2階線形微分方程式のもうひとつの解き方
今回は2階線形微分方程式$$y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)$$
のもうひとつの解法について説明する。未読であれば下記事を読んでから読むことを推奨する。

ロンスキアン
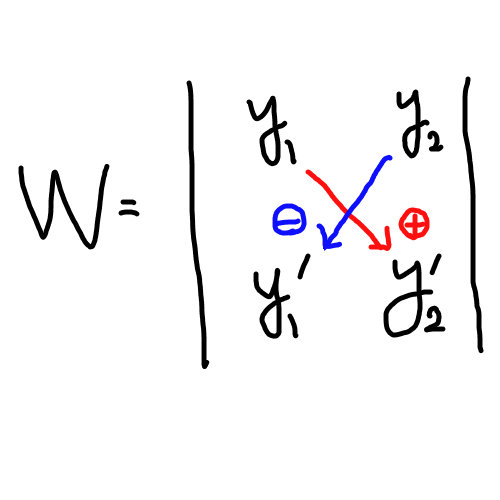
今回説明する解法に登場する ロンスキアン なるものを紹介する。 2階線形微分方程式におけるロンスキアン \(W\) は2つの関数 \(y_1\) , \(y_2\) を使って次の行列式で表される。
$$W\left[\ y_1\ ,y_2\right]=\begin{vmatrix}y_1 & y_2 \\y^{\prime}_1 & y^{\prime}_2 \end{vmatrix}=y_{1}y^{\prime}_{2}-y^{\prime}_{1}y_2$$
例えば、\(y_1=\mathrm{e}^{2x}\)、\(y_2=x\mathrm{e}^{2x}\) の時のロンスキアンは
\begin{eqnarray}W\left[\ \mathrm{e}^{2x},\ x\mathrm{e}^{2x}\right]&=&\begin{vmatrix}\mathrm{e}^{2x} && x\mathrm{e}^{2x}\\ \left(\mathrm{e}^{2x}\right)^{\prime} && \left(x\mathrm{e}^{2x}\right)^{\prime} \end{vmatrix}\\\\&=&\begin{vmatrix}\mathrm{e}^{2x} && x\mathrm{e}^{2x}\\ 2\mathrm{e}^{2x} && \mathrm{e}^{2x}+2x\mathrm{e}^{2x}\end{vmatrix}\\\\&=&\mathrm{e}^{2x}\cdot\left(\mathrm{e}^{2x}+2x\mathrm{e}^{2x}\right)-x\mathrm{e}^{2x}\cdot 2\mathrm{e}^{2x}\\\\&=&\mathrm{e}^{4x}\end{eqnarray}
行列式の計算については次の記事が参考になる。

解法
二階線形微分方程式$$y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)$$
を ロンスキアン を用いて解いていこう。
No.1 : 右辺を0とした式を解く
微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の右辺を0とした式
$$y^{\prime\prime}+ay^{\prime}+by=0$$
を解く。従来通り特性方程式を使って定数 \(C_1\)、\(C_2\) を使って解 \(y_0\) が求まる。解 \(y_0\) において定数 \(C_1\)、\(C_2\) にくっついてる関数を
\(y_1\)、\(y_2\) とする。
ちなみにこの右辺を0とした微分方程式を 斉次方程式 という。
また、
定数 \(C_1\)、\(C_2\) にくっついてる関数
\(y_1\)、\(y_2\) を微分方程式の 基本解 という。
No.2 : ロンスキアンを用いて解が求まる式にぶち込む
No.1 で求めた斉次方程式の解 \(y_1\)、\(y_2\) のロンスキアンを求める。
$$W\left[\ y_1\ ,y_2\right]=\begin{vmatrix}y_1 & y_2 \\y^{\prime}_1 & y^{\prime}_2 \end{vmatrix}=y_{1}y^{\prime}_{2}-y^{\prime}_{1}y_2$$
ロンスキアン \(W\left[\ y_1\ ,y_2\right]\) を用いて与えられた微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の解は次の式で求まる。
$$y=y_1\int\displaystyle\frac{-y_2f\left(x\right)}{W\left[\ y_1\ ,y_2\right]}dx+y_2\int\displaystyle\frac{y_1f\left(x\right)}{W\left[\ y_1\ ,y_2\right]}dx\cdot\cdot\cdot\left(A\right)$$
例題
\(y^{\prime\prime}-4y^{\prime}+3y=\mathrm{e}^{2x}\) を解け。
例題の解答
No.1 : 右辺を0とした式(斉次方程式)を解く
右辺を0とした微分方程式(斉次方程式) \(y^{\prime\prime}-4y^{\prime}+3y=0\) を考える。
特性方程式を解くと
$$\lambda^2-4\lambda+3=0$$
$$\left(\lambda-3\right)\left(\lambda-1\right)=0$$
$$\lambda=\begin{cases}3\\1\end{cases}$$
従って、微分方程式 \(y^{\prime\prime}-4y^{\prime}+3y=0\) の解は定数 \(C_{1}\)、\(C_{2}\) を用いて
$$y_{0}=C_{1}\mathrm{e}^{3x}+C_{2}\mathrm{e}^{x}$$
となる。
解 \(y_0\) において、定数にくっついてる関数(基本解)はそれぞれ
$$y_1=\mathrm{e}^{3x}$$
$$y_2=\mathrm{e}^{x}$$
と求まる。
\(C_{1}\)、\(C_{2}\) にくっついてる関数のどちらを \(y_1\)、\(y_2\) と選んでも構わない。
No.2 : ロンスキアンを用いて解が求まる公式 \(\left(A\right)\) にぶち込む
No.1 で求めた斉次方程式の解 \(y_1=\mathrm{e}^{3x}\)、\(y_2=\mathrm{e}^{x}\) のロンスキアンを求める。
\begin{eqnarray}W\left[\ \mathrm{e}^{3x}\ ,\mathrm{e}^{x}\right]&=&\begin{vmatrix}\mathrm{e}^{3x} & \mathrm{e}^{x} \\\left(\mathrm{e}^{3x}\right)^{\prime} & \left(\mathrm{e}^{x}\right)^{\prime} \end{vmatrix}\\\\&=&\begin{vmatrix}\mathrm{e}^{3x} & \mathrm{e}^{x} \\3\mathrm{e}^{3x}& \mathrm{e}^{x} \end{vmatrix}\\\\&=&\mathrm{e}^{3x}\cdot\mathrm{e}^{x} -\mathrm{e}^{x}\cdot 3\mathrm{e}^{3x}\\\\&=&\mathrm{e}^{4x}-3\mathrm{e}^{4x}\\\\&=&-2\mathrm{e}^{4x}\end{eqnarray}
従って、解が求まる式 \(\left(A\right)\) にぶち込む
\begin{eqnarray}y&=&\mathrm{e}^{3x}\int\displaystyle\frac{-\mathrm{e}^{x}\cdot\mathrm{e}^{2x}}{-2\mathrm{e}^{4x}}dx+\mathrm{e}^{x}\int\displaystyle\frac{\mathrm{e}^{3x}\cdot\mathrm{e}^{2x}}{-2\mathrm{e}^{4x}}dx\\\\&=&\displaystyle\frac{\mathrm{e}^{3x}}{2}\int\mathrm{e}^{-x}dx-\displaystyle\frac{\mathrm{e}^{x}}{2}\int\mathrm{e}^{x}dx\\\\&=&\displaystyle\frac{\mathrm{e}^{3x}}{2}\left(-\mathrm{e}^{-x}+C_A\right)-\displaystyle\frac{\mathrm{e}^{x}}{2}\left(\mathrm{e}^{x}+C_B\right)\\\\&=&-\displaystyle\frac{\mathrm{e}^{2x}}{2}+\displaystyle\frac{C_A}{2}\mathrm{e}^{3x}-\displaystyle\frac{\mathrm{e}^{2x}}{2}-\displaystyle\frac{C_B}{2}\mathrm{e}^{x}\\\\&=&-\mathrm{e}^{2x}+\displaystyle\frac{C_A}{2}\mathrm{e}^{3x}-\displaystyle\frac{C_B}{2}\mathrm{e}^{x}\end{eqnarray}
$$y=-\mathrm{e}^{2x}+\displaystyle\frac{C_A}{2}\mathrm{e}^{3x}-\displaystyle\frac{C_B}{2}\mathrm{e}^{x}$$
練習問題
練習問題1
\(y^{\prime\prime}-3y^{\prime}+2y=2x^2\) を解け。
練習問題2
\(y^{\prime\prime}-4y^{\prime}+4y=\mathrm{e}^{2x}\) を解け。
練習問題3
\(y^{\prime\prime}+2y^{\prime}+5y=\sin{2x}\) を解け。
練習問題4
\(y^{\prime\prime}-5y^{\prime}+6y=\mathrm{e}^{3x}\) を解け。
練習問題5
\(y^{\prime\prime}-2y^{\prime}+2y=\mathrm{e}^{x}\cos{2x}\) を解け。
ひとこと
ロンスキアンを求めて、式(A)にぶち込むだけの問題である。
しかし、注意点として斉次方程式(右辺が0の式)の基本解(2つの解)のどちらを \(y_1\)、\(y_2\) に選ぶかによって ロンスキアン 及び 式(A)での代入の様相が変化することを頭に入れておきたい。
例えば、例題における \(y_1\)、\(y_2\) の選び方として人によっては
$$y_1=\mathrm{e}^{x}$$
$$y_2=\mathrm{e}^{3x}$$
と選ぶ人もいるだろう。このとき、ロンスキアンは
\begin{eqnarray}W\left[\ \mathrm{e}^{x}\ ,\mathrm{e}^{3x}\right]&=&\begin{vmatrix}\mathrm{e}^{x} & \mathrm{e}^{3x} \\\left(\mathrm{e}^{x}\right)^{\prime} & \left(\mathrm{e}^{3x}\right)^{\prime} \end{vmatrix}\\\\&=&\begin{vmatrix}\mathrm{e}^{x} & \mathrm{e}^{3x} \\\mathrm{e}^{x}& 3\mathrm{e}^{3x} \end{vmatrix}\\\\&=&\mathrm{e}^{x}\cdot3\mathrm{e}^{3x} -\mathrm{e}^{3x}\cdot \mathrm{e}^{x}\\\\&=&3\mathrm{e}^{4x}-\mathrm{e}^{4x}\\\\&=&2\mathrm{e}^{4x}\end{eqnarray}
となり「例題の解答」で得たロンスキアンとは符号が反対になっていることがわかる。
そのまま、式(A)にぶちこんで解を求めてみると
\begin{eqnarray}y&=&\mathrm{e}^{x}\int\displaystyle\frac{-\mathrm{e}^{3x}\cdot\mathrm{e}^{2x}}{2\mathrm{e}^{4x}}dx+\mathrm{e}^{3x}\int\displaystyle\frac{\mathrm{e}^{x}\cdot\mathrm{e}^{2x}}{2\mathrm{e}^{4x}}dx\\\\&=&-\displaystyle\frac{\mathrm{e}^{x}}{2}\int\mathrm{e}^{x}dx+\displaystyle\frac{\mathrm{e}^{3x}}{2}\int\mathrm{e}^{-x}dx\\\\&=&-\displaystyle\frac{\mathrm{e}^{x}}{2}\left(\mathrm{e}^{x}+C_A\right)+\displaystyle\frac{\mathrm{e}^{3x}}{2}\left(-\mathrm{e}^{-x}+C_B\right)\\\\&=&-\displaystyle\frac{\mathrm{e}^{2x}}{2}-\displaystyle\frac{C_A}{2}\mathrm{e}^{x}-\displaystyle\frac{\mathrm{e}^{2x}}{2}+\displaystyle\frac{C_B}{2}\mathrm{e}^{3x}\\\\&=&-\mathrm{e}^{2x}-\displaystyle\frac{C_A}{2}\mathrm{e}^{x}+\displaystyle\frac{C_B}{2}\mathrm{e}^{3x}\end{eqnarray}
つまり
$$y=-\mathrm{e}^{2x}+\displaystyle\frac{C_B}{2}\mathrm{e}^{3x}-\displaystyle\frac{C_A}{2}\mathrm{e}^{x}$$
となる。当然 \(C_A\)、\(C_B\) は定数であるのでこれは「例題の解答」で得た解と同じものである。
ここまでを統合すると、基本解としての \(y_1\)、\(y_2\) の選び方によりロンスキアンの符号は変化するが、最終的に得られる解は同じだということが分かる。