ベクトル場の発散 “div”
ベクトル場 \(\pmb{F}\left(x,y,z\right)=F_{1}\ \color{red}{\pmb{i}}+F_{2}\ \color{blue}{\pmb{j}}+F_{3}\ \color{green}{\pmb{k}}\) に対して
$$\mathrm{div}\pmb{F}=\displaystyle\frac{\partial F_{1}}{\partial x}+\displaystyle\frac{\partial F_{2}}{\partial y}+\displaystyle\frac{\partial F_{3}}{\partial z}$$
をベクトル場 \(\pmb{F}\) の 発散 と呼ぶ。
ナブラ ∇ を使った発散 “div”
ハミルトン演算子 \(\pmb{\nabla}\) は
$$\pmb{\nabla}=\displaystyle\frac{\partial}{\partial x}\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial}{\partial y}\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial}{\partial z}\ \color{green}{\pmb{k}}$$
と表される演算子である。

発散 は次のようにナブラ \(\pmb{\nabla}\) とベクトル場 \(\pmb{F}\) の内積で求まる。
\begin{eqnarray}\pmb{\nabla}\cdot\pmb{F}&=&\left(\displaystyle\frac{\partial}{\partial x}\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial}{\partial y}\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial}{\partial z}\ \color{green}{\pmb{k}}\right)\cdot\left(F_{1}\ \color{red}{\pmb{i}}+F_{2}\ \color{blue}{\pmb{j}}+F_{3}\ \color{green}{\pmb{k}}\right)\\\\&=&\displaystyle\frac{\partial F_{1}}{\partial x}\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial F_{2}}{\partial y}\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial F_{3}}{\partial z}\ \color{green}{\pmb{k}}\\\\&=&\mathrm{div}\pmb{F}\end{eqnarray}
$$\pmb{\nabla}\cdot\pmb{F}=\mathrm{div}\pmb{F}$$
発散 “div” の意味
発散 はその符号が正か負かで意味が変わる。
ベクトル場のある点において
\(\mathrm{div}\pmb{F}>0\) のとき、その点においてベクトルが発生していることを意味している。
\(\mathrm{div}\pmb{F}<0\) のときは、その点においてベクトルが収束していることを意味している。
磁石が発する磁場から 発散 とは何かを考えよう。
磁石から出る磁場は小学校の理科で習ったように次の絵のようになる。
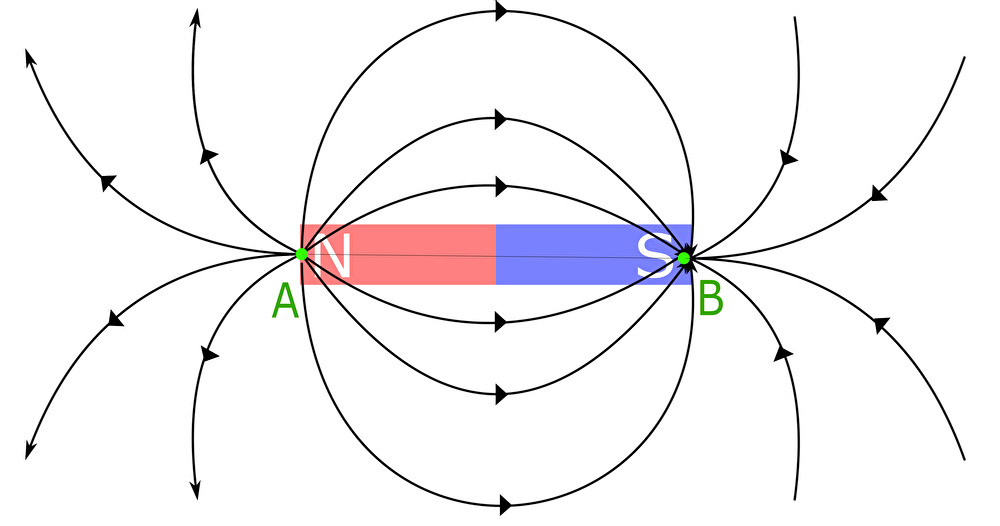
点 \(A\) ではベクトルが生み出されているので、\(\mathrm{div}\pmb{F}\left(A\right)>0\) である。
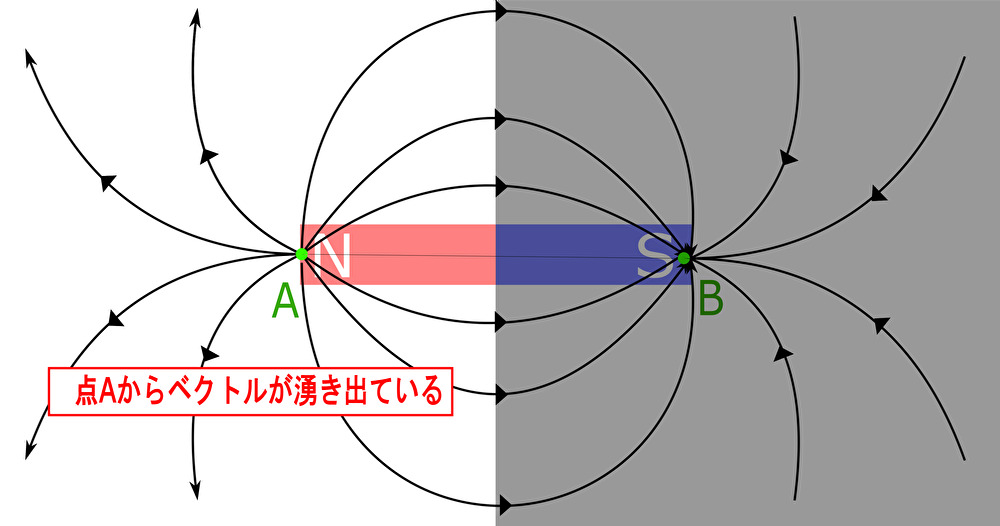
点 \(B\) ではベクトルが吸い込まれているので、\(\mathrm{div}\pmb{F}\left(B\right)<0\) である。
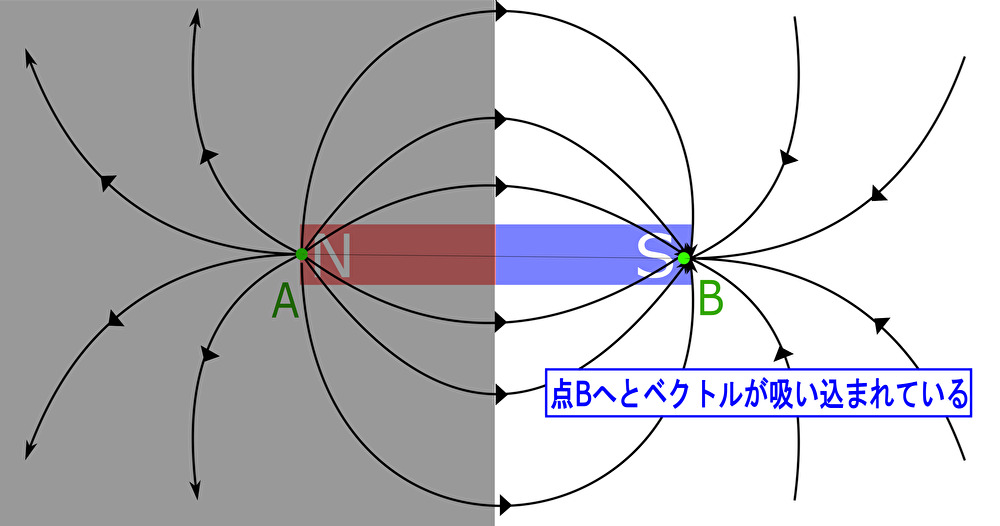
ベクトル場の発散について点 \(A\)、\(B\) のみならず各点について求めて描画すると次のような分布を示す。
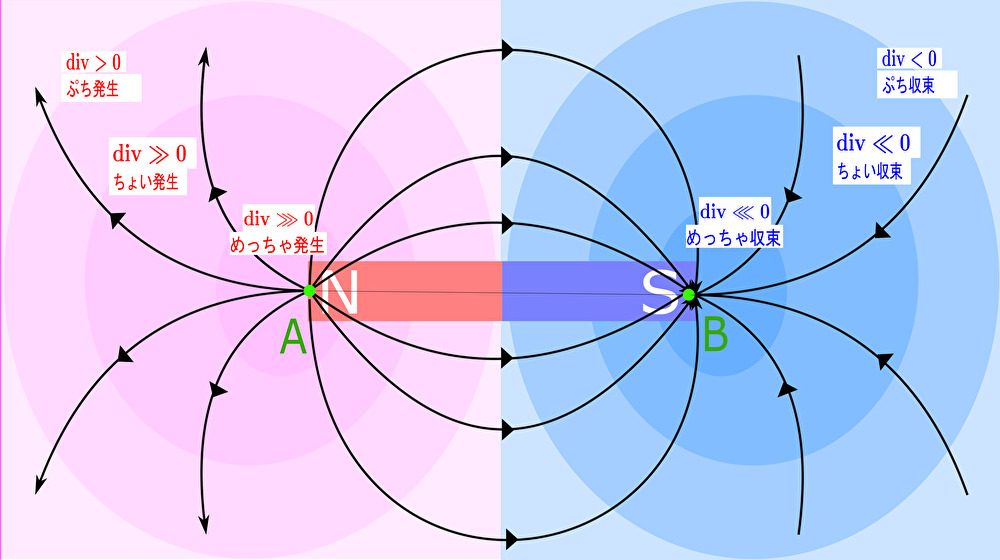
このように 発散 はベクトル場の流れの様子を表現するパラメータであることがわかる。

例題
ベクトル場 \(\pmb{F}\left(x,y,z\right)=x^{2}z\ \color{red}{\pmb{i}}-2xy\ \color{blue}{\pmb{j}}+2yz\ \color{green}{\pmb{k}}\) の発散を求めよ。
例題の解答
偏微分計算をするだけで良い。
ベクトル場 \(\pmb{F}\) の 発散 は
\begin{eqnarray}\mathrm{div}\pmb{F}&=&\displaystyle\frac{\partial}{\partial x}\left(x^{2}z\right)+\displaystyle\frac{\partial}{\partial y}\left(-2xy\right)+\displaystyle\frac{\partial}{\partial z}\left(2yz\right)\\\\&=&\left(2xz\right)+\left(-2x\right)+\left(2y\right)\\\\&=&2xz-2x+2y\end{eqnarray}
$$\mathrm{div}\pmb{F}=2xz-2x+2y$$
練習問題
ベクトル場 \(\pmb{F}\left(x,y,z\right)=2x^{2}y\ \color{red}{\pmb{i}}-xyz^{2}\ \color{blue}{\pmb{j}}+3y^{2}z\ \color{green}{\pmb{k}}\) の点 \(\left(1,1,-1\right)\) における発散を求めよ。
まとめ
・ベクトル場の 発散 は次式で求まる。
$$\mathrm{div}\pmb{F}=\displaystyle\frac{\partial F_{1}}{\partial x}+\displaystyle\frac{\partial F_{2}}{\partial y}+\displaystyle\frac{\partial F_{3}}{\partial z}$$
・\(\mathrm{div}\pmb{F}>0\) はベクトル場の湧きだしを
\(\mathrm{div}\pmb{F}<0\) はベクトル場の流れの消滅を意味する