ベクトル場の回転 “rot”
ベクトル場 \(\pmb{F}\left(x,y,z\right)=F_{1}\ \color{red}{\pmb{i}}+F_{2}\ \color{blue}{\pmb{j}}+F_{3}\ \color{green}{\pmb{k}}\) に対して
$$\mathrm{rot}\pmb{F}=\left(\displaystyle\frac{\partial F_{3}}{\partial y}-\displaystyle\frac{\partial F_{2}}{\partial z}\right)\ \color{red}{\pmb{i}}+\left(\displaystyle\frac{\partial F_{1}}{\partial z}-\displaystyle\frac{\partial F_{3}}{\partial x}\right)\ \color{blue}{\pmb{j}}+\left(\displaystyle\frac{\partial F_{2}}{\partial x}-\displaystyle\frac{\partial F_{1}}{\partial y}\right)\ \color{green}{\pmb{k}}$$
をベクトル場 \(\pmb{F}\) の 回転 と呼ぶ。
ナブラ ∇ を使った回転 “rot”
ハミルトン演算子 \(\pmb{\nabla}\) は
$$\pmb{\nabla}=\displaystyle\frac{\partial}{\partial x}\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial}{\partial y}\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial}{\partial z}\ \color{green}{\pmb{k}}$$
と表される演算子である。

回転 は次のようにナブラ \(\pmb{\nabla}\) とベクトル場 \(\pmb{F}\) の 外積 で求まる。
\begin{eqnarray}\pmb{\nabla}\times\pmb{F}&=&\begin{vmatrix}\pmb{i} & \pmb{j} & \pmb{k}\\\displaystyle\frac{\partial}{\partial x} & \displaystyle\frac{\partial}{\partial y} & \displaystyle\frac{\partial}{\partial z}\\F_{1} & F_{2} & F_{3}\end{vmatrix}\\\\&=&\left(\displaystyle\frac{\partial F_{3}}{\partial y}-\displaystyle\frac{\partial F_{2}}{\partial z}\right)\ \color{red}{\pmb{i}}+\left(\displaystyle\frac{\partial F_{1}}{\partial z}-\displaystyle\frac{\partial F_{3}}{\partial x}\right)\ \color{blue}{\pmb{j}}+\left(\displaystyle\frac{\partial F_{2}}{\partial x}-\displaystyle\frac{\partial F_{1}}{\partial y}\right)\ \color{green}{\pmb{k}}\\\\&=&\mathrm{rot}\pmb{F}\end{eqnarray}
外積計算は下記事参照

\begin{eqnarray}\pmb{\nabla}\times\pmb{F}&=&\mathrm{rot}\pmb{F}\end{eqnarray}
回転 “rot” の意味
回転 “rot” は ベクトル場 の 流れの回転の様子 を意味している。
\(\mathrm{rot}>0\) のとき、ベクトル場は反時計回りに回転している。
\(\mathrm{rot}<0\) のとき、ベクトル場は時計回りに回転している。
\(\mathrm{rot}=0\) のとき、ベクトル場は回転していない。
ことを意味する。
さて理科で習った 右ねじの法則 によると鉛直正方向に電流 \(I\) が流れているとき、反時計回り方向に磁界が発生する。
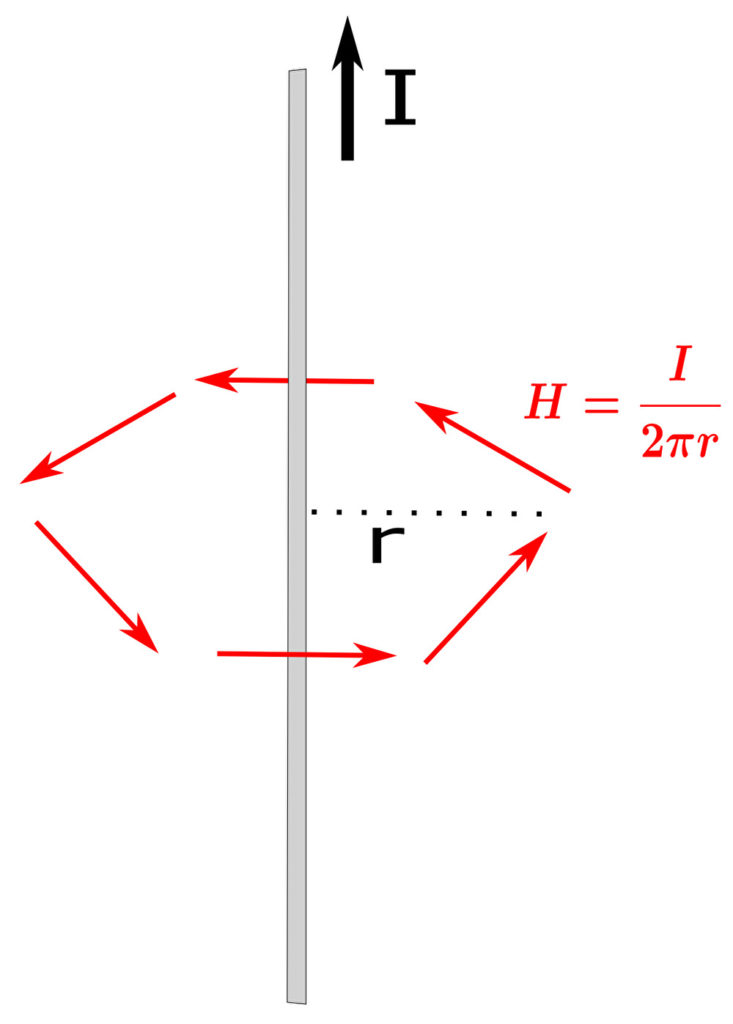
つまり、この磁界のベクトル場の回転 \(\mathrm{rot}\pmb{H}\) は 正 であることがわかる。
例題
ベクトル場 \(\pmb{F}\left(x,y,z\right)=x^{2}z\ \color{red}{\pmb{i}}-2xy\ \color{blue}{\pmb{j}}+2yz\ \color{green}{\pmb{k}}\) の回転を求めよ。
例題の解答
ベクトル場の 回転 は先述の通り、∇と ベクトル場の 外積 で求まるので、
\begin{eqnarray}\mathrm{rot}\pmb{F}&=&\pmb{\nabla}\times\pmb{F}\\\\&=&\begin{vmatrix}\pmb{i} & \pmb{j} & \pmb{k}\\\displaystyle\frac{\partial}{\partial x} & \displaystyle\frac{\partial}{\partial y} & \displaystyle\frac{\partial}{\partial z}\\x^{2}z & -2xy & 2yz\end{vmatrix}\\\\&=&\left(\displaystyle\frac{\partial}{\partial y}\left(2yz\right)-\displaystyle\frac{\partial}{\partial z}\left(-2xy\right)\right)\ \color{red}{\pmb{i}}+\left(\displaystyle\frac{\partial}{\partial z}\left(x^{2}z\right)-\displaystyle\frac{\partial}{\partial x}\left(2yz\right)\right)\ \color{blue}{\pmb{j}}+\left(\displaystyle\frac{\partial}{\partial x}\left(-2xy\right)-\displaystyle\frac{\partial}{\partial y}\left(x^{2}z\right)\right)\ \color{green}{\pmb{k}}\\\\&=&\left(2z-0\right)\ \color{red}{\pmb{i}}+\left(x^{2}-0\right)\ \color{blue}{\pmb{j}}+\left(-2y-0\right)\ \color{green}{\pmb{k}}\\\\&=&2z\ \color{red}{\pmb{i}}+x^{2}\ \color{blue}{\pmb{j}}-2y\ \color{green}{\pmb{k}}\end{eqnarray}
\begin{eqnarray}\mathrm{rot}\pmb{F}&=&2z\ \color{red}{\pmb{i}}+x^{2}\ \color{blue}{\pmb{j}}-2y\ \color{green}{\pmb{k}}\end{eqnarray}
練習問題
ベクトル場 \(\pmb{F}\left(x,y,z\right)=2x^{2}y\ \color{red}{\pmb{i}}-xyz^{2}\ \color{blue}{\pmb{j}}+3y^{2}z\ \color{green}{\pmb{k}}\) の点 \(\left(1,1,-1\right)\) における回転を求めよ。
まとめ
・ベクトル場の 回転 は次式で求まる。
\begin{eqnarray}\pmb{\nabla}\times\pmb{F}&=&\mathrm{rot}\pmb{F}\\\\&=&\begin{vmatrix}\pmb{i} & \pmb{j} & \pmb{k}\\\displaystyle\frac{\partial}{\partial x} & \displaystyle\frac{\partial}{\partial y} & \displaystyle\frac{\partial}{\partial z}\\F_{1} & F_{2} & F_{3}\end{vmatrix}\\\\&=&\left(\displaystyle\frac{\partial F_{3}}{\partial y}-\displaystyle\frac{\partial F_{2}}{\partial z}\right)\ \color{red}{\pmb{i}}+\left(\displaystyle\frac{\partial F_{1}}{\partial z}-\displaystyle\frac{\partial F_{3}}{\partial x}\right)\ \color{blue}{\pmb{j}}+\left(\displaystyle\frac{\partial F_{2}}{\partial x}-\displaystyle\frac{\partial F_{1}}{\partial y}\right)\ \color{green}{\pmb{k}}\end{eqnarray}
・\(\mathrm{rot}\pmb{F}>0\) は反時計回りの
\(\mathrm{rot}\pmb{F}<0\) は時計回りのベクトル場の流れを意味する





