スカラー3重積とその計算
ベクトル \(\pmb{a}\)、\(\pmb{b}\)、\(\pmb{c}\) に対して
$$\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}$$
または
$$\pmb{a}\cdot\left( \pmb{b}\times\pmb{c}\right)$$
をベクトル \(\pmb{a}\)、\(\pmb{b}\)、\(\pmb{c}\) の スカラー3重積 と呼び、記号を省略して \(\left(\pmb{a},\pmb{b},\pmb{c}\right)\) と書くこともある。内積の交換法則よりこれら2つの式は等しく
$$\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}= \pmb{a}\cdot\left( \pmb{b}\times\pmb{c}\right)$$
が成り立つ。
\(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\)、\(\pmb{b}=\left(b_{1},b_{2},b_{3}\right)\)、\(\pmb{c}=\left(c_{1},c_{2},c_{3}\right)\) と成分を設定して スカラー3重積 を計算してみよう。ここでは、1つ目の スカラー3重積 のみ計算する。
まず、\(\pmb{a}\times\pmb{b}\) は
\begin{eqnarray}&&\pmb{a}\times\pmb{b}\\\\&=&\begin{vmatrix}\pmb{i} & \pmb{j} & \pmb{k}\\a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\end{vmatrix}\\\\&=&\left(a_{2}b_{3}-a_{3}b_{2}\right)\pmb{i}+\left(a_{3}b_{1}-a_{1}b_{3}\right)\pmb{j}+\left(a_{1}b_{2}-a_{2}b_{1}\right)\pmb{k}\end{eqnarray}
と計算される。外積 計算については下記事参照。

次に、外積 \(\pmb{a}\times\pmb{b}\) とベクトル \(\pmb{c}\) の内積は
\begin{eqnarray}&&\left(\pmb{a}\times\pmb{b}\right)\cdot\color{green}{\pmb{c}}\\\\&=&\{\left(a_{2}b_{3}-a_{3}b_{2}\right)\pmb{i}+\left(a_{3}b_{1}-a_{1}b_{3}\right)\pmb{j}+\left(a_{1}b_{2}-a_{2}b_{1}\right)\pmb{k}\}\cdot\color{green}{\{c_{1}\pmb{i}+c_{2}\pmb{j}+c_{3}\pmb{k}\}}\\\\&=&\left(a_{2}b_{3}-a_{3}b_{2}\right)\color{green}{c_{1}}+\left(a_{3}b_{1}-a_{1}b_{3}\right)\color{green}{c_{2}}+\left(a_{1}b_{2}-a_{2}b_{1}\right)\color{green}{c_{3}}\\\\&=&\color{green}{c_{1}}\left(a_{2}b_{3}-a_{3}b_{2}\right)+\color{green}{c_{2}}\left(a_{3}b_{1}-a_{1}b_{3}\right)+\color{green}{c_{3}}\left(a_{1}b_{2}-a_{2}b_{1}\right)\end{eqnarray}
ここで、サラスの方法より
\begin{cases}\begin{vmatrix}a_{2} & a_{3}\\b_{2} & b_{3} \end{vmatrix}=a_{2}b_{3}-a_{3}b_{2}\\\\-\begin{vmatrix}a_{1} & a_{3}\\b_{1} & b_{3} \end{vmatrix}=-\left(a_{1}b_{3}-a_{3}b_{1}\right)=a_{3}b_{1}-a_{1}b_{3}\\\\\begin{vmatrix}a_{1} & a_{2}\\b_{1} & b_{2} \end{vmatrix}=a_{1}b_{2}-a_{2}b_{1}\end{cases}
であるので、スカラー3重積 の各項はこれら 行列式 を用いて
\begin{eqnarray}&&\left(\pmb{a}\times\pmb{b}\right)\cdot\color{green}{\pmb{c}}\\\\&=&\color{green}{c_{1}}\left(a_{2}b_{3}-a_{3}b_{2}\right)+\color{green}{c_{2}}\left(a_{3}b_{1}-a_{1}b_{3}\right)+\color{green}{c_{3}}\left(a_{1}b_{2}-a_{2}b_{1}\right)\\\\&=&\color{green}{c_{1}}\begin{vmatrix}a_{2} & a_{3}\\b_{2} & b_{3} \end{vmatrix}+\color{green}{c_{2}}\left[-\begin{vmatrix}a_{1} & a_{3}\\b_{1} & b_{3} \end{vmatrix}\right]+\color{green}{c_{3}}\begin{vmatrix}a_{1} & a_{2}\\b_{1} & b_{2} \end{vmatrix}\\\\&=&\color{green}{c_{1}}\begin{vmatrix}a_{2} & a_{3}\\b_{2} & b_{3} \end{vmatrix}-\color{green}{c_{2}}\begin{vmatrix}a_{1} & a_{3}\\b_{1} & b_{3} \end{vmatrix}+\color{green}{c_{3}}\begin{vmatrix}a_{1} & a_{2}\\b_{1} & b_{2} \end{vmatrix}\end{eqnarray}
と書き直される。
この 行列式 が係数付きで足し算となっている形は 余因子展開 で見られる形であり、余因子展開 の符号も考慮して
\begin{eqnarray}&&\left(\pmb{a}\times\pmb{b}\right)\cdot\color{green}{\pmb{c}}\\\\&=&\color{green}{c_{1}}\begin{vmatrix}a_{2} & a_{3}\\b_{2} & b_{3} \end{vmatrix}-\color{green}{c_{2}}\begin{vmatrix}a_{1} & a_{3}\\b_{1} & b_{3} \end{vmatrix}+\color{green}{c_{3}}\begin{vmatrix}a_{1} & a_{2}\\b_{1} & b_{2} \end{vmatrix}\\\\&=&\left(-1\right)^{3+1}\color{green}{c_{1}}\begin{vmatrix}a_{2} & a_{3}\\b_{2} & b_{3} \end{vmatrix}+\left(-1\right)^{3+2}\color{green}{c_{2}}\begin{vmatrix}a_{1} & a_{3}\\b_{1} & b_{3} \end{vmatrix}+\left(-1\right)^{3+3}\color{green}{c_{3}}\begin{vmatrix}a_{1} & a_{2}\\b_{1} & b_{2} \end{vmatrix}\\\\&=&\begin{vmatrix}a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\\ \color{green}{c_{1}} & \color{green}{c_{2}} & \color{green}{c_{3}} \end{vmatrix}\end{eqnarray}
と計算される。

従って、スカラー3重積 は各ベクトルの成分を並べた \(3\times 3\) 行列式であることが分かる。
$$\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}= \pmb{a}\cdot\left( \pmb{b}\times\pmb{c}\right)=\begin{vmatrix}a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\\c_{1} & c_{2} & c_{3} \end{vmatrix}$$
となる。
スカラー3重積の図形的意味
スカラー3重積 \(\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}\) は図形的にはベクトル \(\pmb{a}\)、\(\pmb{b}\)、\(\pmb{c}\) で張られた 平行六面体の体積 を意味する。
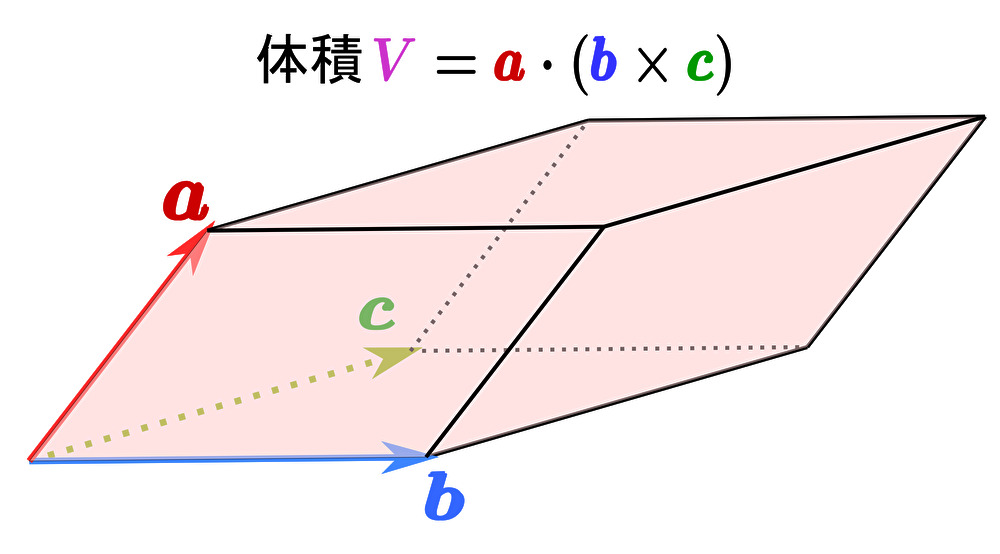
スカラー3重積 が平行六面体の体積であることの証明
まず底面のベクトル \(\pmb{b}\)、\(\pmb{c}\) で張られた平行四辺形の面積 \(S\) を求めよう。
ベクトル \(\pmb{b}\)、\(\pmb{c}\) のなす角を \(\alpha\) とすると、\(\pmb{b}\)、\(\pmb{c}\) が作る三角形の面積を \(T\) としたとき
$$T=\frac{1}{2}|\pmb{b}||\pmb{c}|\sin{\alpha}$$
と求まる。
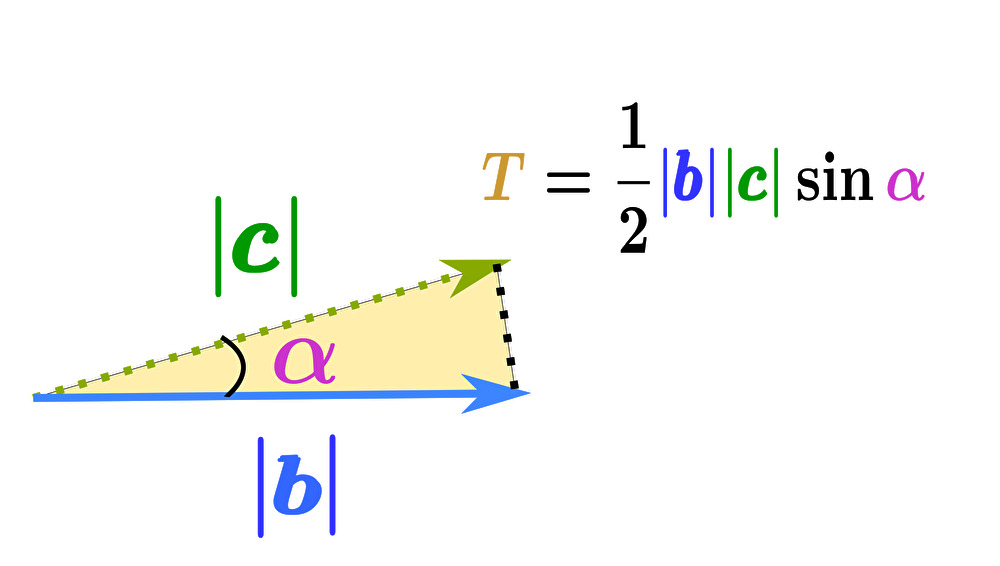
底面の平行四辺形 \(S\) はこの三角形 \(T\) の2つ分の面積なので
\begin{eqnarray}S&=&2T\\\\&=&2\cdot\frac{1}{2}|\pmb{b}||\pmb{c}|\sin{\alpha}\\\\&=&|\pmb{b}||\pmb{c}|\sin{\alpha}\end{eqnarray}
と求まる。

ここで、\(|\pmb{b}||\pmb{c}|\sin{\alpha}=|\pmb{b}\times\pmb{c}|\) であるので平行四辺形の面積は 外積 で表現されて
\begin{eqnarray}S&=&|\pmb{b}||\pmb{c}|\sin{\alpha}\\\\&=&\pmb{b}\times\pmb{c}\end{eqnarray}
と書ける。
次に、平行六面体の高さ \(h\) を求めよう。
ベクトル \(\pmb{a}\) と高さ方向の軸となす角を \(\theta\) と置くと
平行六面体の体積 \(h\) は
$$h=|\pmb{a}|\cos{\theta}$$
と書ける。
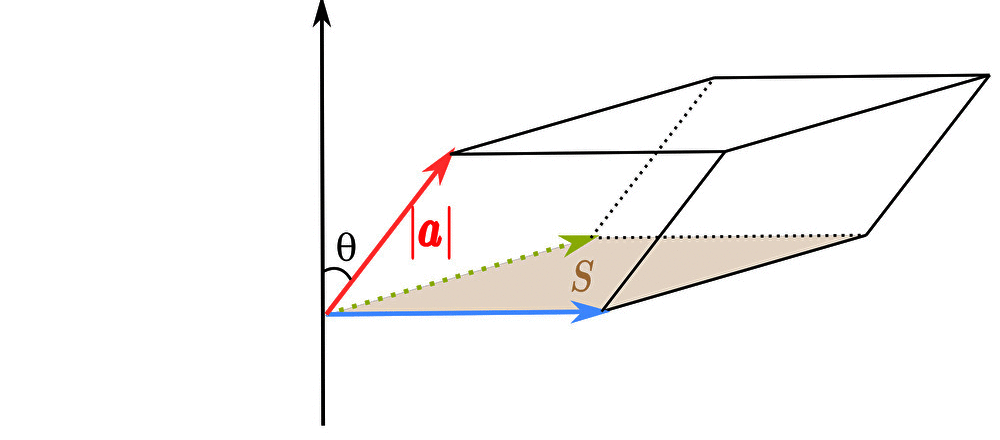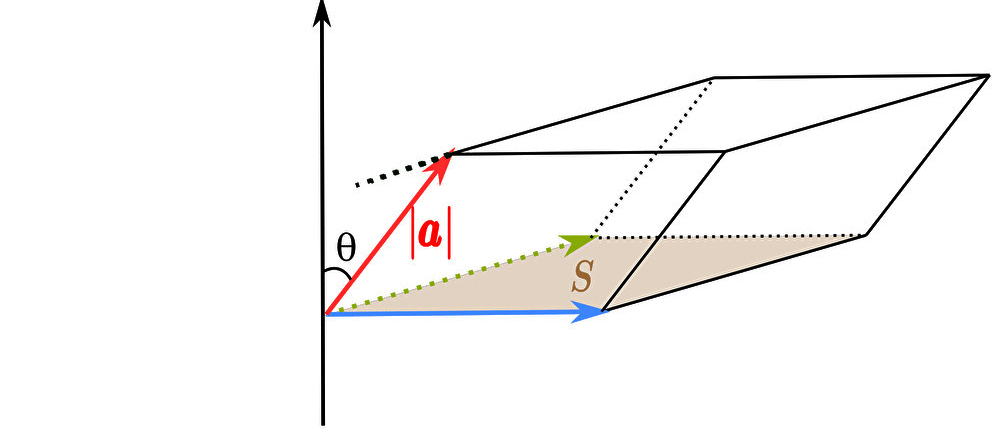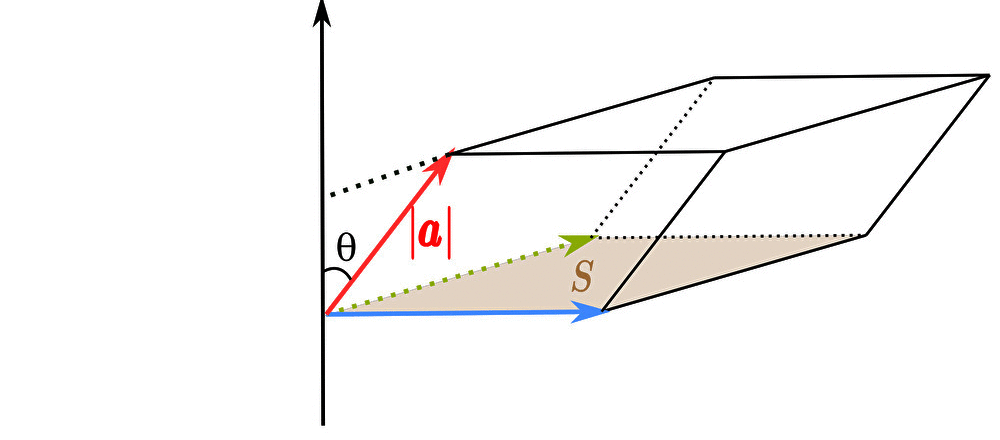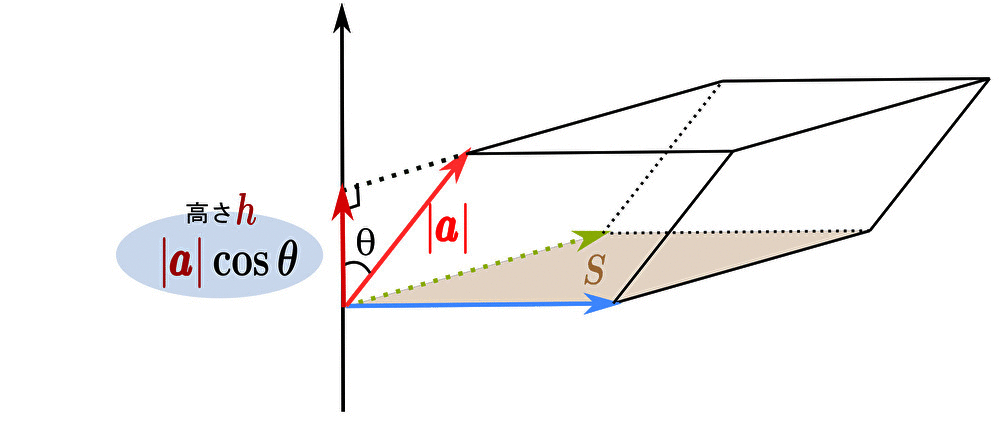
したがって、平行六面体の体積 \(V\) は底面積と高さの掛け算で求まり
\begin{eqnarray}V&=&Sh\\\\&=&|\pmb{b}\times\pmb{c}||\pmb{a}|\cos{\theta}\end{eqnarray}
さて 外積 \(\pmb{b}\times\pmb{c}\) の方向はベクトル \(\pmb{b}\)、\(\pmb{c}\) と垂直な方向である。すなわち、平行六面体の高さ方向と等しい。

すなわち 外積 \(\pmb{b}\times\pmb{c}\) とベクトル \(\alpha\) と高さ方向の軸とベクトル \(\alpha\) がなす角がなす角は等しく \(\theta\) である。
すなわち、\(V\) の右辺について
$$|\pmb{b}\times\pmb{c}||\pmb{a}|\cos{\theta}=\left(\pmb{b}\times\pmb{c}\right)\cdot\pmb{a}$$
であるので
\begin{eqnarray}V&=&|\pmb{b}\times\pmb{c}||\pmb{a}|\cos{\theta}\\\\&=&\left(\pmb{b}\times\pmb{c}\right)\cdot\pmb{a}\\\\&=&\pmb{a}\cdot\left(\pmb{b}\times\pmb{c}\right)\end{eqnarray}
となり、スカラー3重積 は 平行六面体の体積 であることが示された。
3重積の計算結果が “スカラー” であることが 「スカラー3重積」 と呼ばれる所以である。
例題
ベクトル \(\pmb{a}\)、\(\pmb{b}\)、\(\pmb{c}\) の スカラー3重積 を \(\left(\pmb{a},\pmb{b},\pmb{c}\right)\) と書く時
\(\left(\pmb{a},\pmb{b},\pmb{c}\right)=-\left(\pmb{b},\pmb{a},\pmb{c}\right)\)
を示せ。
例題の解答
スカラー3重積 は行列式で表現されて
\begin{eqnarray}\left(\pmb{a},\pmb{b},\pmb{c}\right)&=&\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}\\\\&=&\begin{vmatrix}a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\\c_{1} & c_{2} & c_{3} \end{vmatrix}\end{eqnarray}
行列式 は \(-1\) 倍することで行を入れ替えることができる性質を持つ。
すなわち
\begin{eqnarray}\left(\color{red}{\pmb{a}},\color{blue}{\pmb{b}},\color{green}{\pmb{c}}\right)&=&\begin{vmatrix}\color{red}{a_{1}} & \color{red}{a_{2}} & \color{red}{a_{3}}\\\color{blue}{b_{1}} & \color{blue}{b_{2}} & \color{blue}{b_{3}}\\\color{green}{c_{1}} & \color{green}{c_{2}} & \color{green}{c_{3}} \end{vmatrix}\\\\&=&\begin{vmatrix}\color{blue}{b_{1}} & \color{blue}{b_{2}} & \color{blue}{b_{3}}\\ \color{red}{a_{1}} & \color{red}{a_{2}} & \color{red}{a_{3}}\\ \color{green}{c_{1}} & \color{green}{c_{2}} & \color{green}{c_{3}} \end{vmatrix}\\\\&=&-\left(\color{blue}{\pmb{b}},\color{red}{\pmb{a}},\color{green}{\pmb{c}}\right)\end{eqnarray}
まとめ
・スカラー3重積 は各ベクトルの成分を並べた \(3\times 3\) 行列式である。
・スカラー3重積 \(\left( \pmb{a}\times\pmb{b}\right)\cdot \pmb{c}\) はベクトル \(\pmb{a}\)、\(\pmb{b}\)、\(\pmb{c}\) で張られた 平行六面体の体積 を意味する。