曲面とは
1変数のベクトル(関数)が描く軌跡は 曲線 であった。
一方、2変数のベクトル(関数)が描く軌跡は 曲面 である。
例えば、次の2変数ベクトル関数の 曲面 を考えてみよう。
$$\pmb{r}=\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\ \ \ \ \ (\ 0\leq u\leq \pi)$$
各成分について
\begin{eqnarray}x\left(u,v\right)&=&\sin{u}\cos{v}\\\\y\left(u,v\right)&=&\sin{u}\sin{v}\\\\z\left(u,v\right)&=&\cos{u}\end{eqnarray}
である。ここから媒介変数 \(u\)、\(v\) を消去していく。
\(x\) 成分と \(y\) 成分は共に \(\sin{u}\) を因数として持っており、それぞれ \(\cos{v}\) 、\(\sin{v}\) を有している。
そのため、\(\cos^{2}{\theta}+\sin^{2}{\theta}=1\) が使えそうだなと判断して、この2成分の二乗和で計算できそうだなと考えられる。
\begin{eqnarray}x^{2}+y^{2}&=&\sin^{2}{u}\cos^{2}{v}+\sin^{2}{u}\sin^{2}{v}\\\\&=&\sin^{2}{u}\left(\cos^{2}{v}+\sin^{2}{v}\right)\\\\&=&\sin^{2}{u}\cdot 1\\\\&=&\sin^{2}{u}\end{eqnarray}
となり、\(\sin{u}\) の二乗へと変形された。
一方、\(z=\cos{u}\) であるので、再度 \(\cos^{2}{\theta}+\sin^{2}{\theta}=1\) は使えそうであり
\begin{eqnarray}\left(x^{2}+y^{2}\right)+z^{2}&=&\sin^{2}{u}+\cos^{2}{u}\\\\&=&1\end{eqnarray}
すなわち、先ほどのベクトル関数
$$\pmb{r}=\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\ \ \ \ \ (0\leq u\leq 2\pi\ ,\ 0\leq v\leq 2\pi$$
は \(u\)、\(v\) を消去して表現すると次の式になる。
$$x^{2}+y^{2}+z^{2}=1$$
これは正しく 半径 \(1\) の 球表面 であり、2変数ベクトル関数が 曲面(曲がった面)を意味するものだと確認できる。
接平面と法線ベクトル
曲線 に沿った直線を 接線 と呼ぶように、曲面 に沿った平面を 接平面 と呼ぶ。
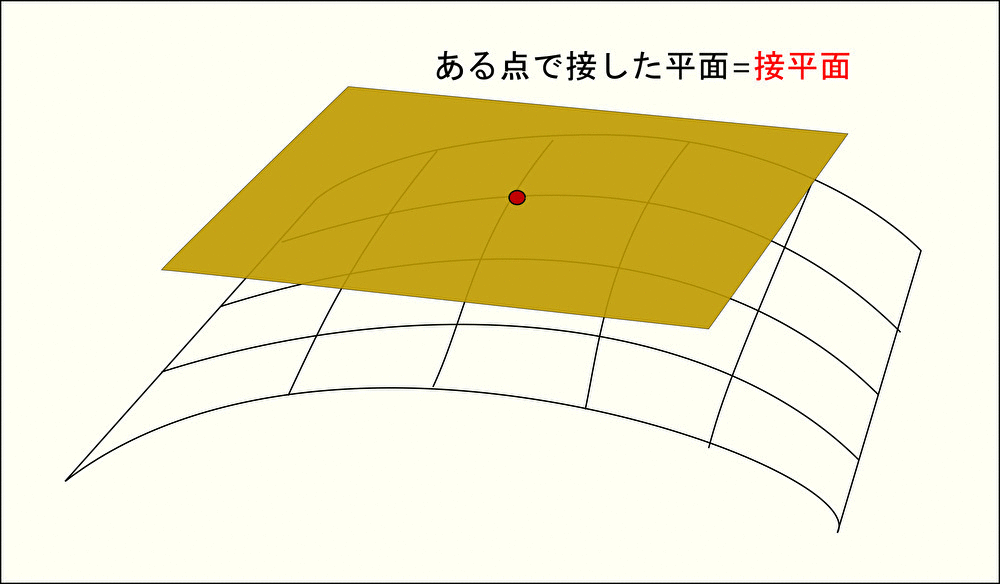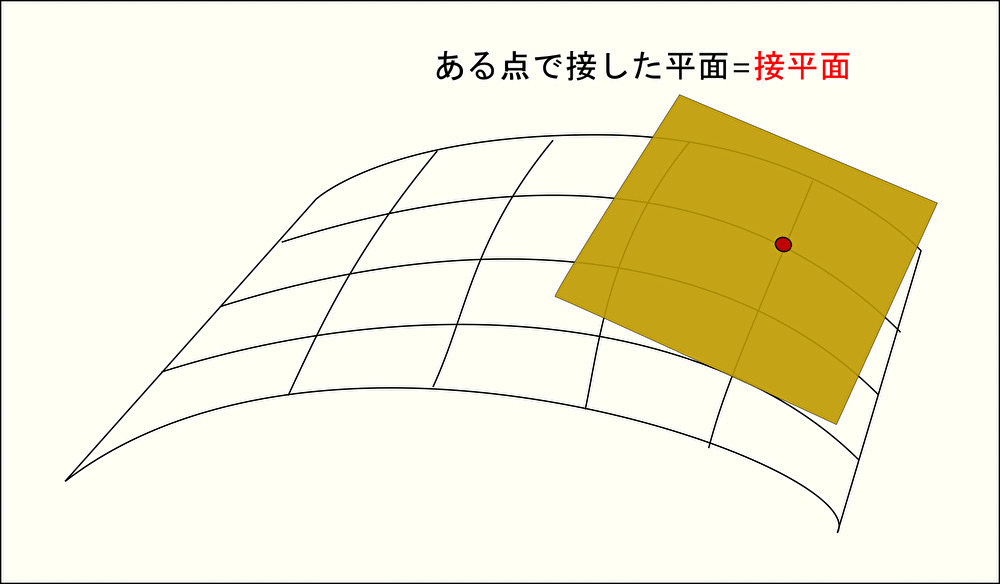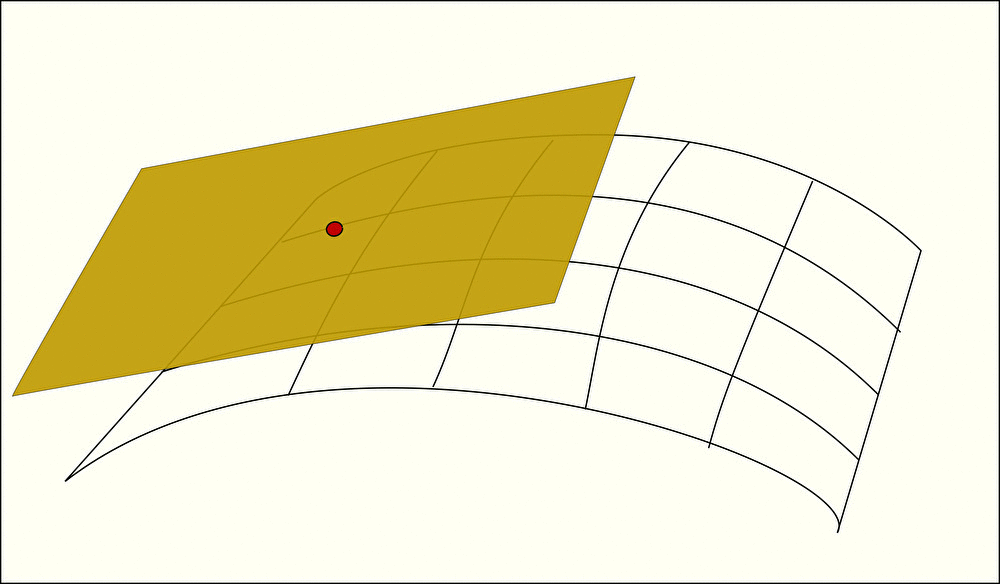
また、接平面 と垂直なベクトルを 法線ベクトル と呼ぶ。法線ベクトルは接平面と垂直であることから、曲面に対して垂直なベクトルであることがわかる。
法線ベクトル を求めるには、まず曲面の式 \(\pmb{r}\) を2変数 \(u\)、\(v\) それぞれで偏微分してあげることから始まる。
求まった偏微分 \(\displaystyle\frac{\partial\pmb{r}}{\partial u}\)、\(\displaystyle\frac{\partial\pmb{r}}{\partial v}\) はそれぞれ接平面上の互いに垂直なベクトルを示す。
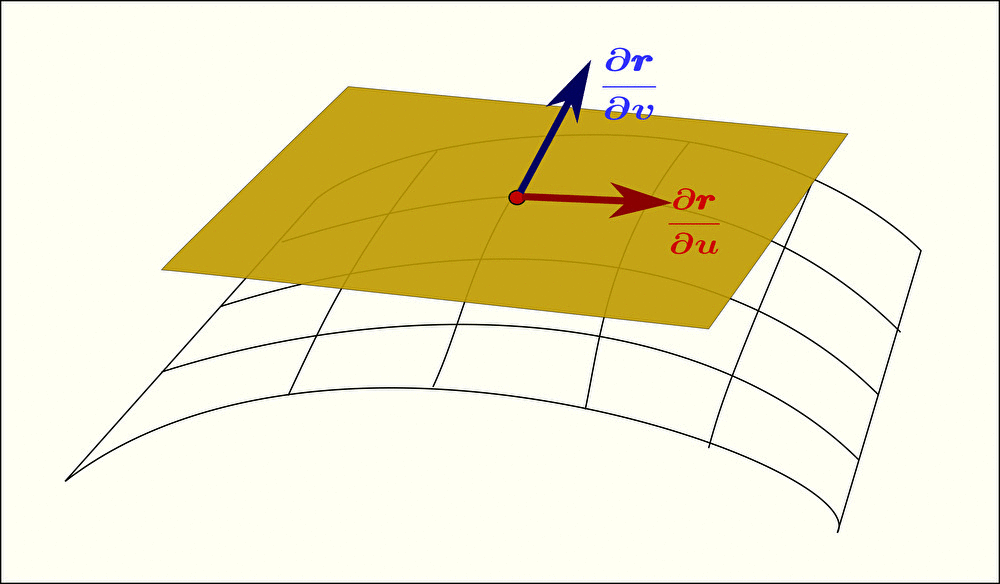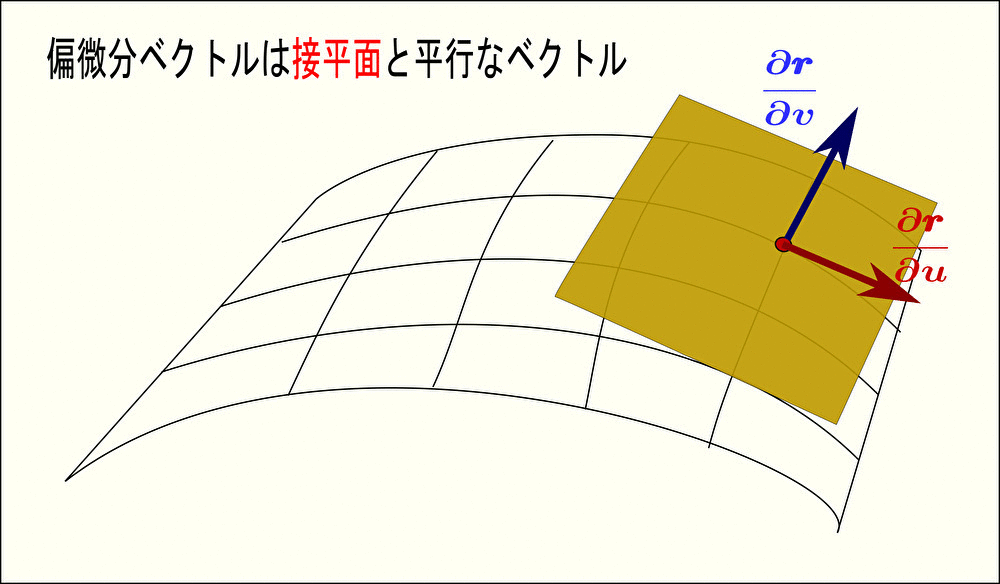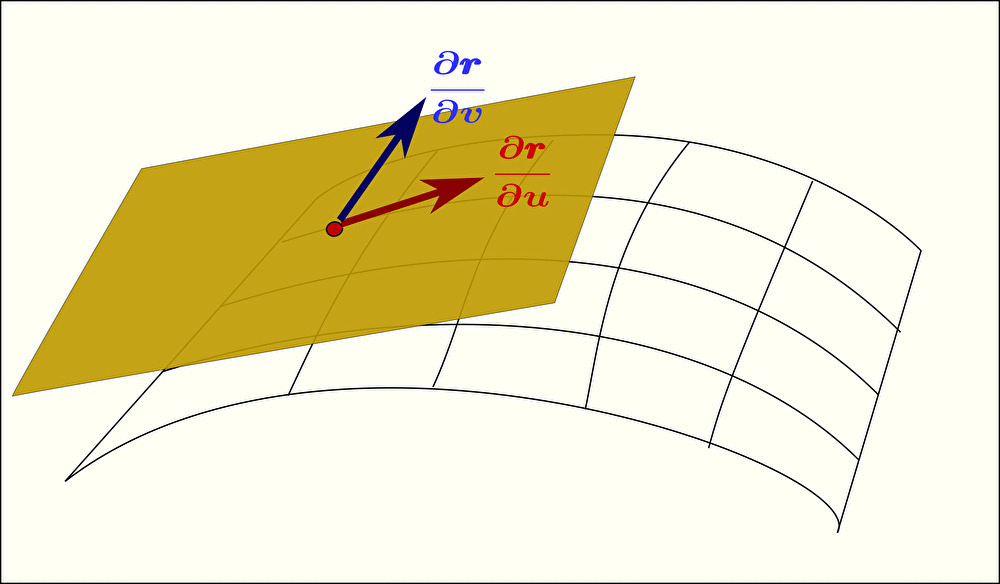
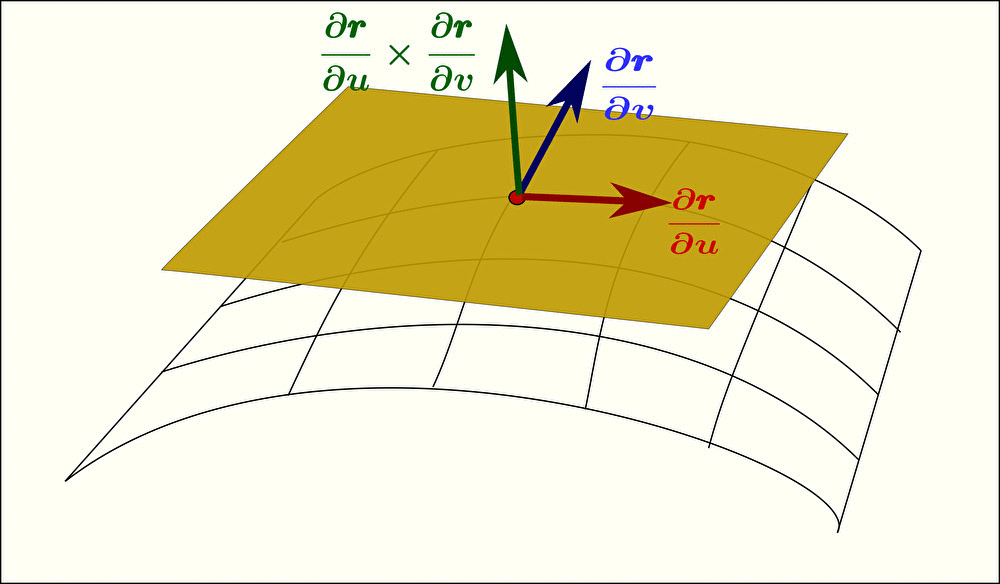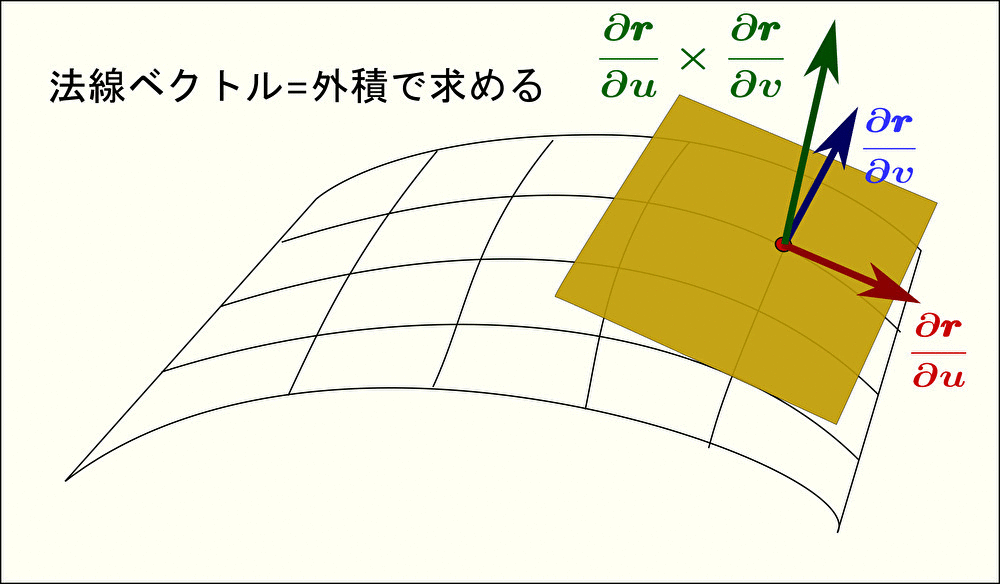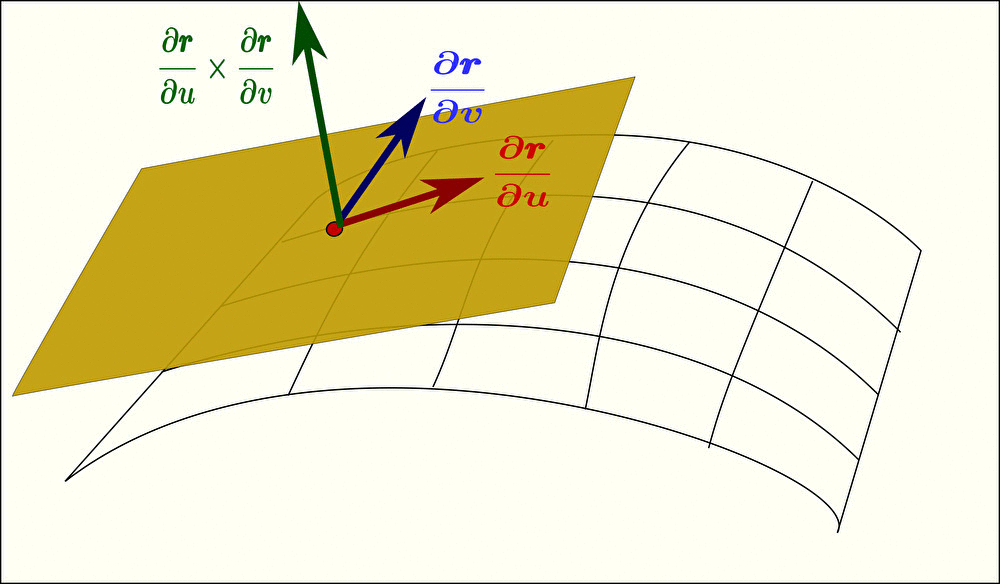
すなわち、面に平行な2つのベクトル \(\displaystyle\frac{\partial\pmb{r}}{\partial u}\)、\(\displaystyle\frac{\partial\pmb{r}}{\partial v}\) どうしで外積をとることで、法線ベクトル(面に垂直な方向のベクトル)を求めることができる。
例えば、曲面 \(\pmb{r}=u\ \color{red}{\pmb{i}}+v\ \color{blue}{\pmb{j}}+\left(1-u^{2}-v^{2}\right)\ \color{green}{\pmb{k}}\) の法線ベクトルを求めてみよう。
この曲線は次のような 放物面(パラボラアンテナ形)である。
次の手順に沿うことで 法線ベクトル を求めることができる。
No.1 : 曲面の式を \(u\)、\(v\) で偏微分する。
まず、曲面の式を \(u\)、\(v\) で 偏微分 すると
$$\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}=\ \color{red}{\pmb{i}}-2u\ \color{green}{\pmb{k}}$$
$$\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}=\ \color{blue}{\pmb{j}}-2v\ \color{green}{\pmb{k}}$$
となる。
この2つの動径を偏微分したベクトルは、先述の通り 放物面 に 接する平面 上の 互いに垂直なベクトル である。
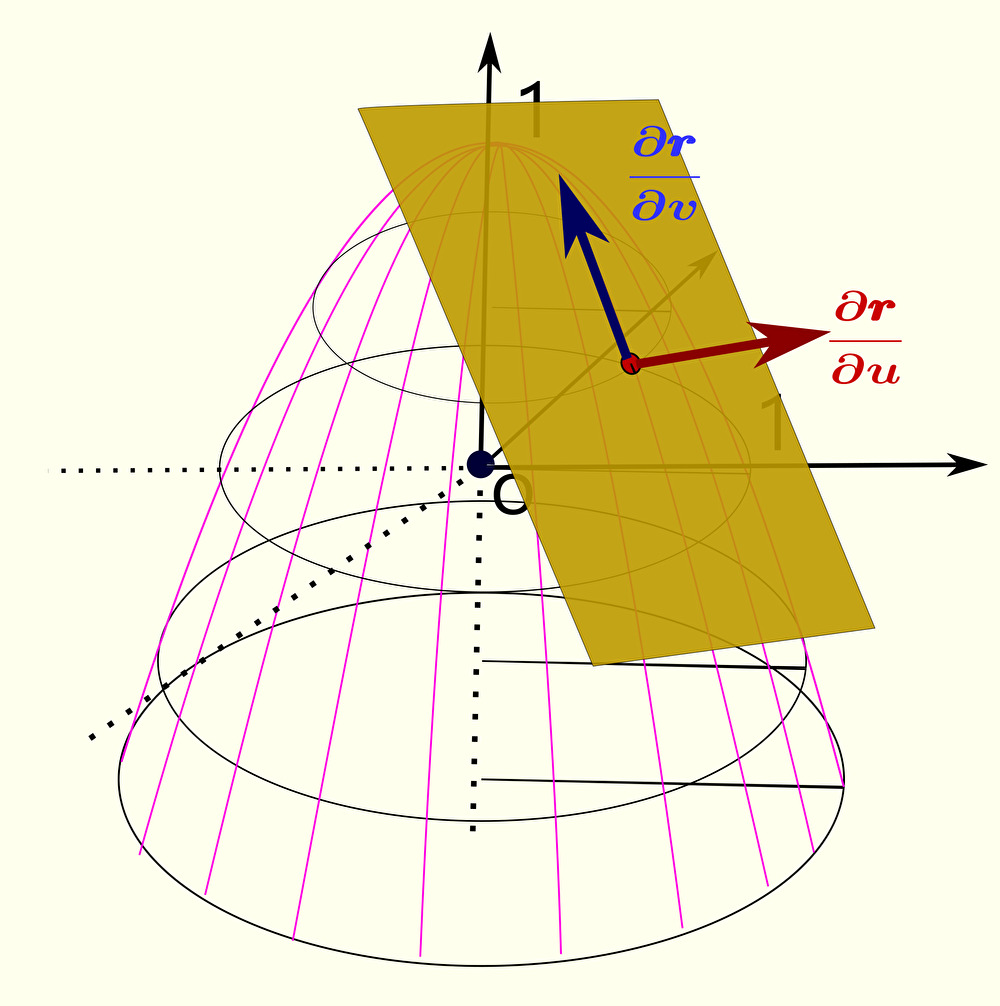
No.2 : 求めた \(\displaystyle\frac{\partial\pmb{r}}{\partial u}\) と \(\displaystyle\frac{\partial\pmb{r}}{\partial v}\) どうしで外積をとる
2つの偏微分ベクトルどうしで外積をとると
\begin{eqnarray}\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}\times\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}&=&\begin{vmatrix} \color{red}{\pmb{i}} & \color{blue}{\pmb{j}} & \color{green}{\pmb{k}} \\ 1 & 0 & -2u \\ 0 & 1 & -2v \end{vmatrix}\\\\&=&\{0\cdot\left(-2v\right)-\left(-2u\right)\cdot 1\}\ \color{red}{\pmb{i}}+\{\left(-2u\right)\cdot 0-1\cdot \left(-2v\right)\}\ \color{blue}{\pmb{j}}+\{1\cdot 1-0\cdot 0\}\ \color{green}{\pmb{k}}\\\\&=&2u\ \color{red}{\pmb{i}}+2v\ \color{blue}{\pmb{j}}+\ \color{green}{\pmb{k}}\end{eqnarray}
となる。外積計算については下記事参照。

2つの 偏微分ベクトル は 接平面 上のベクトルなので、これらの外積は接平面と垂直な方向となり、下図のように 接平面 と 垂直な方向 のベクトル(法線ベクトル)を得る。
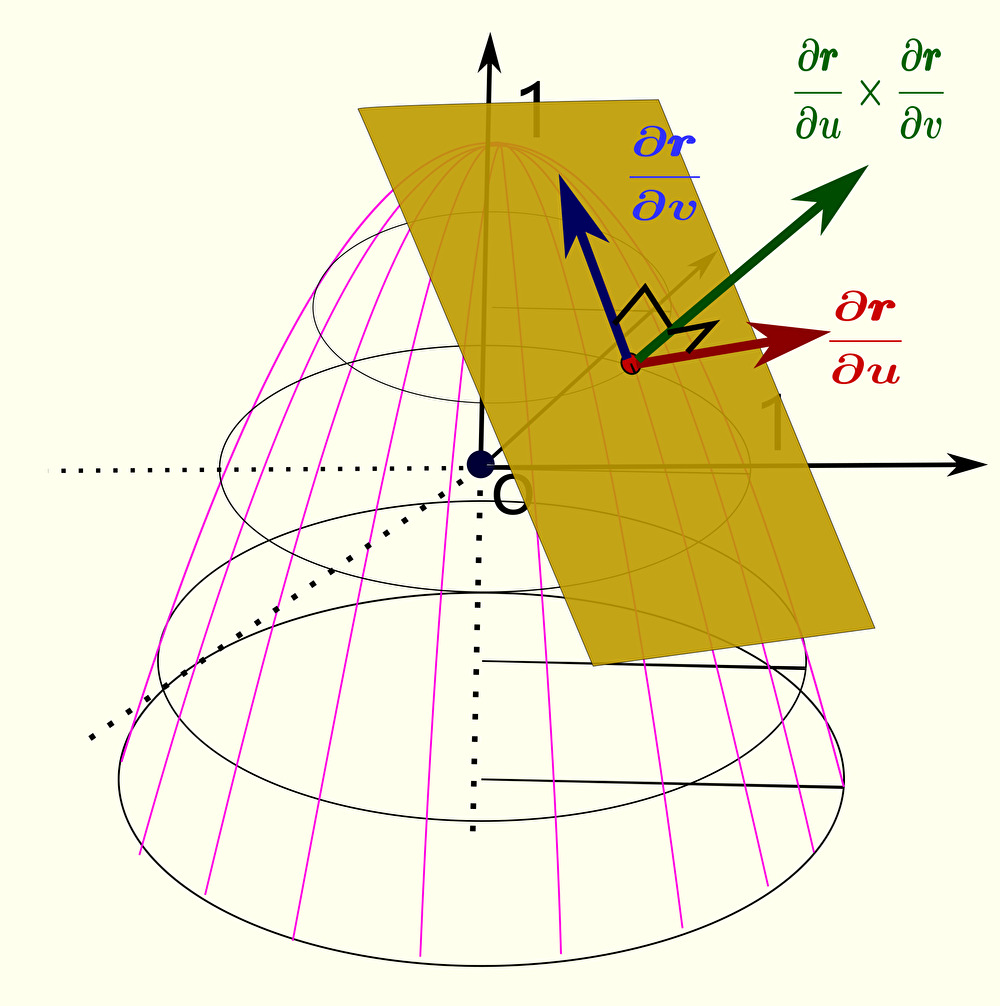
以上より求める法線ベクトルは
$$2u\ \color{red}{\pmb{i}}+2v\ \color{blue}{\pmb{j}}+\ \color{green}{\pmb{k}}$$
例題
単位球面 \(\pmb{r}=\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\ \ \ \ \ (\ 0\leq u\leq \pi)\) の単位法線ベクトルを求めよ。
例題の解答
No.1 : 曲面の式を \(u\)、\(v\) で偏微分する。
球面の式 \(\pmb{r}=\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\ \ \ \ \ (\ 0\leq u\leq \pi)\) を \(u\) と \(v\) でそれぞれ偏微分すると
$$\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}=\cos{u}\cos{v}\ \color{red}{\pmb{i}}+\cos{u}\sin{v}\ \color{blue}{\pmb{j}}-\sin{u}\ \color{green}{\pmb{k}}$$
\begin{eqnarray}\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}&=&-\sin{u}\sin{v}\ \color{red}{\pmb{i}}+\sin{u}\cos{v}\ \color{blue}{\pmb{j}}+0\ \color{green}{\pmb{k}}\\\\&=&-\sin{u}\sin{v}\ \color{red}{\pmb{i}}+\sin{u}\cos{v}\ \color{blue}{\pmb{j}}\end{eqnarray}
No.2 : 求めた \(\displaystyle\frac{\partial\pmb{r}}{\partial u}\) と \(\displaystyle\frac{\partial\pmb{r}}{\partial v}\) どうしで外積をとる
2つの偏微分ベクトルどうしで外積をとると
\begin{eqnarray}\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}\times\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}&=&\begin{vmatrix} \color{red}{\pmb{i}} & \color{blue}{\pmb{j}} & \color{green}{\pmb{k}} \\ \cos{u}\cos{v} & \cos{u}\sin{v} & -\sin{u} \\ -\sin{u}\sin{v} & \sin{u}\cos{v} & 0 \end{vmatrix}\\\\&=&\{\cos{u}\sin{v} \cdot 0-\left(-\sin{u}\right)\cdot\sin{u}\cos{v}\}\ \color{red}{\pmb{i}}\\\\&&+\{\left( -\sin{u}\right)\cdot\left(-\sin{u}\sin{v}\right)-\cos{u}\cos{v}\cdot 0\}\ \color{blue}{\pmb{j}}\\\\&&+\{\cos{u}\cos{v}\cdot\sin{u}\cos{v}-\cos{u}\sin{v}\cdot\left(-\sin{u}\sin{v}\right)\}\ \color{green}{\pmb{k}}\\\\&=&\{\sin^{2}{u}\cos{v}\}\ \color{red}{\pmb{i}}+\{\sin^{2}{u}\sin{v}\}\ \color{blue}{\pmb{j}}+\{\sin{u}\cos{u}\cos^{2}{v}+\sin{u}\cos{u}\sin^{2}{v}\}\ \color{green}{\pmb{k}}\\\\&=&\{\sin^{2}{u}\cos{v}\}\ \color{red}{\pmb{i}}+\{\sin^{2}{u}\sin{v}\}\ \color{blue}{\pmb{j}}+\sin{u}\cos{u}\{\cos^{2}{v}+\sin^{2}{v}\}\ \color{green}{\pmb{k}}\\\\&=&\sin^{2}{u}\cos{v}\ \color{red}{\pmb{i}}+\sin^{2}{u}\sin{v}\ \color{blue}{\pmb{j}}+\sin{u}\cos{u}\ \color{green}{\pmb{k}}\ \ \ \color{green}{\left(\cos^{2}{v}+\sin^{2}{v}=1 より\right)}\end{eqnarray}
となり法線ベクトルが求まる。
次に今回求めたいものは 「単位」法線ベクトルであるので、先ほど求めた法線ベクトルを自身の大きさで割って「単位ベクトル化」する必要がある。
法線ベクトルの大きさは
\begin{eqnarray}\left|\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}\times\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}\right|&=&\left|\sin^{2}{u}\cos{v}\ \color{red}{\pmb{i}}+\sin^{2}{u}\sin{v}\ \color{blue}{\pmb{j}}+\sin{u}\cos{u}\ \color{green}{\pmb{k}}\right|\\\\&=&\sqrt{\left(\sin^{2}{u}\cos{v}\right)^{2}+\left(\sin^{2}{u}\sin{v}\right)^{2}+\left(\sin{u}\cos{u}\right)^{2}}\\\\&=&\sqrt{\sin^{4}{u}\cos^{2}{v}+\sin^{4}{u}\sin^{2}{v}+\sin^{2}{u}\cos^{2}{u}}\\\\&=&\sqrt{\sin^{4}{u}\left(\cos^{2}{v}+\sin^{2}{v}\right)+\sin^{2}{u}\cos^{2}{u}}\\\\&=&\sqrt{\sin^{4}{u}+\sin^{2}{u}\cos^{2}{u}}\ \ \ \color{green}{\left(\cos^{2}{v}+\sin^{2}{v}=1 より\right)}\\\\&=&\sqrt{\sin^{2}{u}\left(\sin^{2}{u}+\cos^{2}{u}\right)}\\\\&=&\sqrt{\sin^{2}{u}}\ \ \ \color{green}{\left(\cos^{2}{v}+\sin^{2}{v}=1 より\right)}\\\\&=&\color{red}{\sin{u}}\end{eqnarray}
したがって、求める単位法線ベクトルは
\begin{eqnarray}\displaystyle\frac{\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}\times\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}}{\left|\color{magenta}{\displaystyle\frac{\partial\pmb{r}}{\partial u}}\times\color{blue}{\displaystyle\frac{\partial\pmb{r}}{\partial v}}\right|}&=&\displaystyle\frac{\sin^{2}{u}\cos{v}\ \color{red}{\pmb{i}}+\sin^{2}{u}\sin{v}\ \color{blue}{\pmb{j}}+\sin{u}\cos{u}\ \color{green}{\pmb{k}}}{\sin{u}}\\\\&=&\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\end{eqnarray}
と求まる。
$$\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}$$
練習問題
曲面 \(\pmb{r}=\sin{u}\cos{v}\ \color{red}{\pmb{i}}+\sin{u}\sin{v}\ \color{blue}{\pmb{j}}+\cos{u}\ \color{green}{\pmb{k}}\ \ \ \ \ (\ 0\leq u\leq \pi)\) の単位法線ベクトルを求めよ。
まとめ
・1変数のベクトル関数 は「曲線」を意味するが、2変数のベクトル関数 は「曲面」を意味する。
・曲面の式を 偏微分 & 外積 計算するだけで 法線ベクトル を求めることができる。