線積分とは
高校数学で習った積分について思い出してみよう。
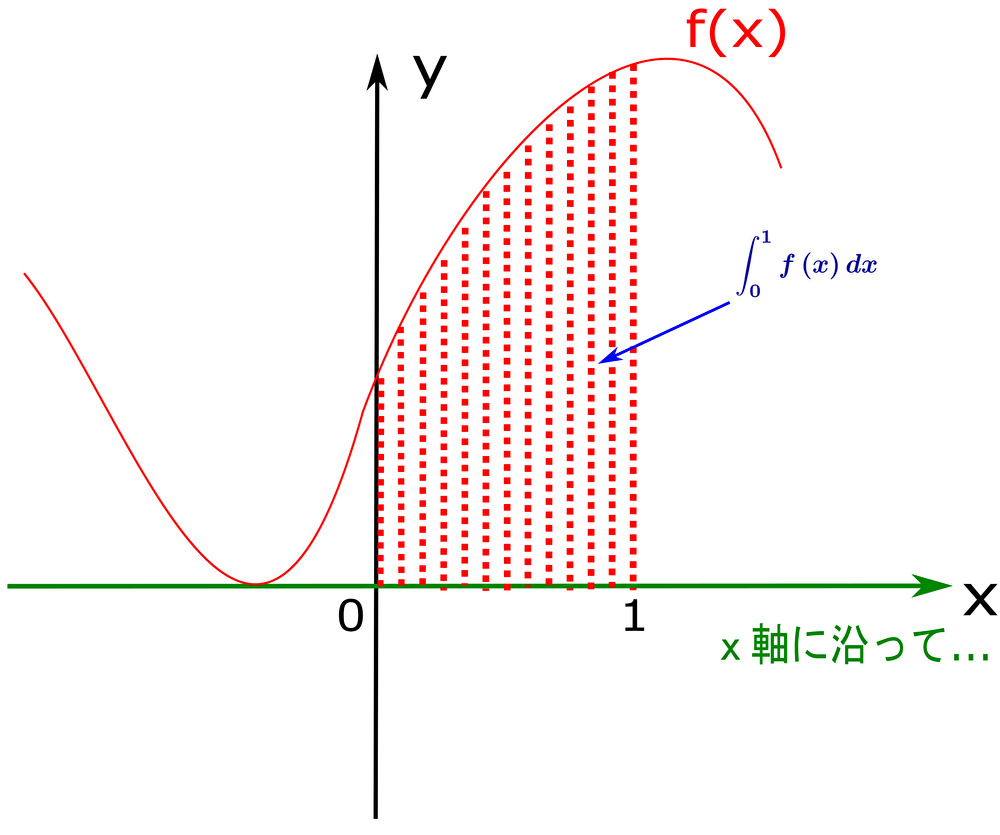
$$\int^{1}_{0} f\left(x\right) dx$$
これは、関数 \(f\left(x\right)\) を \(x\) 軸に沿った積分をしていた。
3次元で見ると次のようになる。

このように、高校までの積分は あくまで \(x\) 軸方向の経路に沿って積分していた。
線積分 はこの 積分の経路が曲線になった(経路の自由度が上がった)ものだと考えて良い。
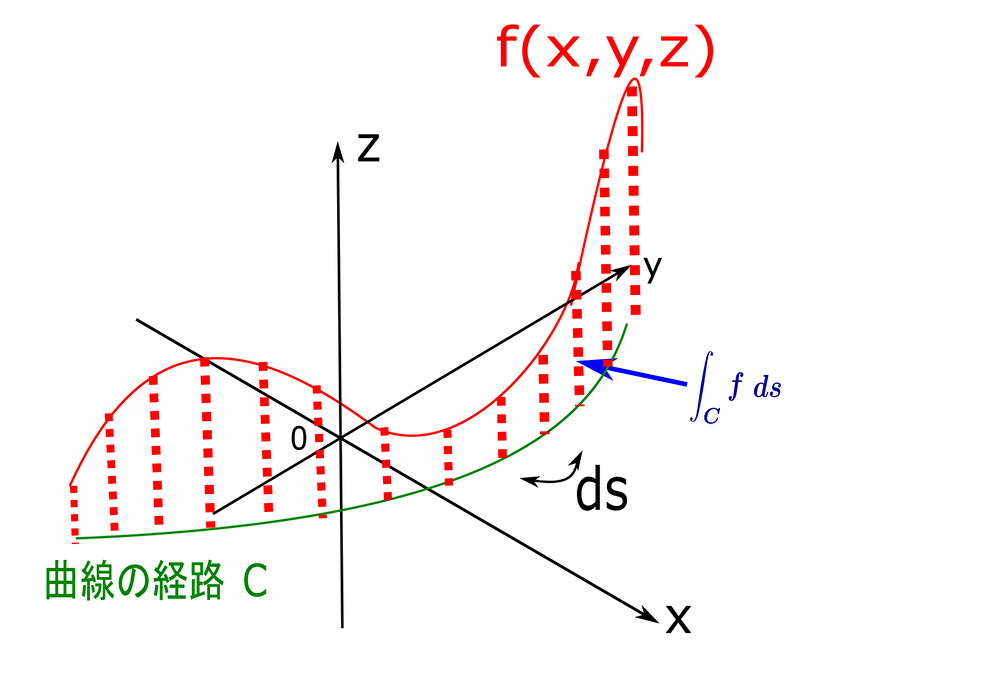
この曲線の積分経路の微小変化分の大きさを 線素 と呼び、\(ds\) とあらわす。
曲線 \(C\) に沿った 線積分 はこの 線素 \(ds\) を用いて
$$\int_{C} f\left(x,y,z\right) ds$$
と書くことが多い。
スカラー線積分の計算
線積分の計算は 関数 \(f\left(x,y,z\right)\) と 線素 \(ds\) を変数 \(t\) で統一して表現することで、\(t\) のみの積分へと置き換えられる。
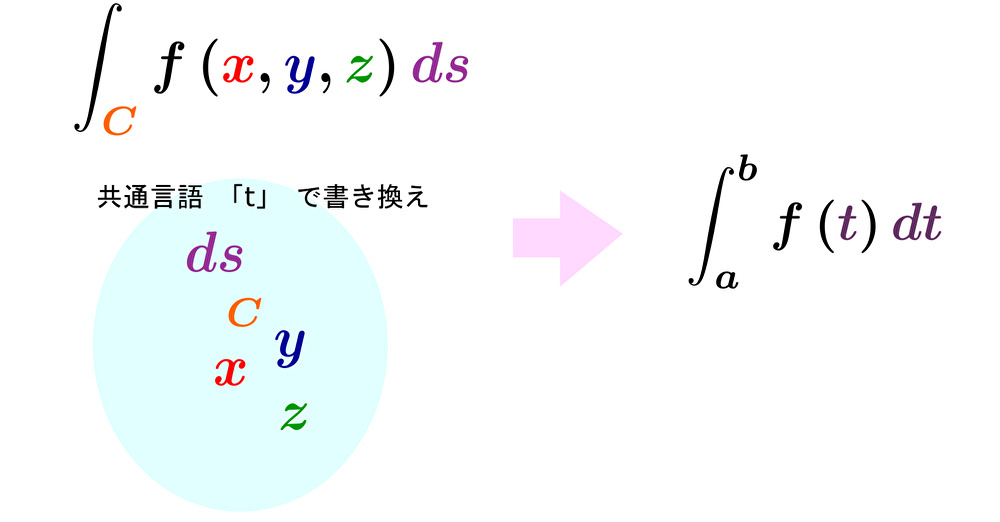
例として、 原点から点 \(A\left(6,8,10\right)\) へと向かう線分 を \(C\) とした時の
関数 \(f\left(x,y,z\right)=x+y+z\) を積分経路 \(C\) に沿って積分してみよう
Step1 : 積分経路 \(C\) を 「\(t\)」 で書き換え
積分経路 \(C\) は原点から点 \(A\left(6,8,10\right)\) へと向かう線分ということで、変数 \(t\) \(\left(0\leq t \leq 1\right)\) を使うと、
線分 \(C\) 上の点 \(P\) の \(x\)成分、\(y\)成分、\(z\)成分はそれぞれ
\begin{cases}x\left(t\right)&=&6t\\\\y\left(t\right)&=&8t\ \ \ \ \left(0\leq t \leq 1\right)\\\\z\left(t\right)&=&10t\end{cases}
と表現できる。

線分 \(C\) 上の点 \(P\) の座標が
\(x:y:z=6:8:10\)
であることがわかっている前提で記述した
Step2 : 積分経路 \(C\) の線素 \(ds\) を 「\(t\)」 で書き換え
積分経路 \(C\) の線素ベクトル \(d\pmb{s}\) を \(t\) を使って書く。
まず、\(ds\) を \(dt\) について倍分(約分の逆)変形することで、\(t\) を無理やり登場させる。
$$ds=\displaystyle\frac{ds}{dt}dt$$
これより生まれた \(\displaystyle\frac{ds}{dt}\) を求める。
まず、積分経路 \(C\) 上の点 \(P\) を表す位置ベクトル \(\pmb{
r}\) は Step1 で求めた、\(x\)、\(y\)、\(z\) 成分 より
$$\pmb{r}=6t\ \color{red}{\pmb{i}}+8t\ \color{blue}{\pmb{j}}+10t\ \color{green}{\pmb{k}}$$
と表される。
次に、位置ベクトルの微小変化ベクトル \(d\pmb{r}\) を求める。
位置ベクトル \(\pmb{r}\) と 微量だけ伸ばした \(\pmb{r}+d\pmb{r}\) は下図のように示される。

この二つのベクトルの差が位置ベクトルの微小変化ベクトル \(d\pmb{r}\) である。
さて、線素 とは 積分経路の微小変化分の大きさ であった。
つまり、線素 \(ds\) は微小変化ベクトル \(d\pmb{r}\) の大きさであるので
$$ds=|d\pmb{r}|$$
という関係が成り立つ。
つまり本題の \(\displaystyle\frac{ds}{dt}\) については
\begin{eqnarray}\displaystyle\frac{ds}{dt}&=&\displaystyle\frac{\left|d\pmb{r}\right|}{dt}\\\\&=&\left|\displaystyle\frac{d\pmb{r}}{dt}\right|\ \left(dt はスカラーより\ dt=|dt|\right)\\\\&=&\left|\displaystyle\frac{d}{dt}\left(6t\ \color{red}{\pmb{i}}+8t\ \color{blue}{\pmb{j}}+10t\ \color{green}{\pmb{k}}\right)\right|\\\\&=&\left|6\ \color{red}{\pmb{i}}+8\ \color{blue}{\pmb{j}}+10\ \color{green}{\pmb{k}}\right|\\\\&=&\sqrt{6^{2}+8^{2}+10^{2}}\\\\&=&10\sqrt{2}\end{eqnarray}
と求まる。
つまるところ
$$ds=10\sqrt{2}dt$$
と求まる。
Step1 と Step2 より元の線積分は次のように書き換えられる。
\begin{eqnarray}\displaystyle\int_{C}f\left(x,y,z\right)ds&=&\displaystyle\int_{0}^{1}f\left(x,y,z\right)10\sqrt{2}dt\end{eqnarray}
Step3 : \(f\left(x,y,z\right)=x+y+z\) も 「\(t\)」 で書き換え
\(f\left(x,y,z\right)=x+y+z\) も \(t\) で書き換える。
Step1 で求めた積分経路上の点 \(P\) の各成分を代入すると
\begin{eqnarray}f\left(x,y,z\right)&=&x+y+z\\\\&=&6t+8t+10t\\\\&=&24t\end{eqnarray}
Step4 : 全員集合して計算!!
Step1 ~ Step3 で変換した \(t\) の式を統合すると
\begin{eqnarray}\displaystyle\int_{C}\left(x+y+z\right)ds&=&\displaystyle\int_{0}^{1}24t\cdot 10\sqrt{2}dt\\\\&=&\displaystyle\int_{0}^{1}\left(240\sqrt{2}t\right)dt\\\\&=&240\sqrt{2}\left[\displaystyle\frac{t^{2}}{2}\right]^{1}_{0}\\\\&=&120\sqrt{2}\end{eqnarray}
$$120\sqrt{2}$$
例題
積分経路を \(C\ :\ \pmb{r}=t^{2}\ \color{red}{\pmb{i}}+t\ \color{blue}{\pmb{j}}\ \left(0\leq t\leq 1\right)\) に沿って
スカラー関数 \(f\left(x,y,z\right)=xy+yz+zx\) を線積分せよ。
例題の解答
Step1 : 積分経路 \(C\) を 「\(t\)」 で書き換え
積分経路は \(C\ :\ \pmb{r}=t^{2}\ \color{red}{\pmb{i}}+t\ \color{blue}{\pmb{j}}\ \left(0\leq t\leq 1\right)\) で設定されているので
経路 \(C\) 上の点 \(P\) の \(x\)成分、\(y\)成分、\(z\)成分はそれぞれ
\begin{cases}x\left(t\right)&=&t^{2}\\\\y\left(t\right)&=&t\ \ \ \ \left(0\leq t \leq 1\right)\\\\z\left(t\right)&=&0\end{cases}
と表される。
Step2 : 積分経路 \(C\) の線素 \(ds\) を 「\(t\)」 で書き換え
まず、 \(\displaystyle\frac{ds}{dt}\) を求めよう。
\begin{eqnarray}\displaystyle\frac{ds}{dt}&=&\displaystyle\frac{\left|d\pmb{r}\right|}{dt}\\\\&=&\left|\displaystyle\frac{d\pmb{r}}{dt}\right|\ \left(dt はスカラーより\ dt=|dt|\right)\\\\&=&\left|\displaystyle\frac{d}{dt}\left(t^{2}\ \color{red}{\pmb{i}}+t\ \color{blue}{\pmb{j}}+0\ \color{green}{\pmb{k}}\right)\right|\\\\&=&\left|2t\ \color{red}{\pmb{i}}+1\ \color{blue}{\pmb{j}}+0\ \color{green}{\pmb{k}}\right|\\\\&=&\sqrt{\left(2t\right)^{2}+1^{2}}\\\\&=&\sqrt{4t^{2}+1}\end{eqnarray}
つまるところ、 \(ds=\displaystyle\frac{ds}{dt}dt\) であるので
$$ds=\sqrt{4t^{2}+1}dt$$
Step3 : \(f\left(x,y,z\right)=xy+yz+zx\) も 「\(t\)」 で書き換え
\(f\left(x,y,z\right)=xy+yz+zx\) も \(t\) で書き換える。
Step1 で求めた積分経路上の点 \(P\) の各成分を代入すると
\begin{eqnarray}f\left(x,y,z\right)&=&xy+yz+zx\\\\&=&t^{2}\cdot t+t\cdot 0+0\cdot t^{2}\\\\&=&t^{3}\end{eqnarray}
Step4 : 全員集合して計算!!
Step1 ~ Step3 で変換した \(t\) の式を統合すると
\begin{eqnarray}\displaystyle\int_{C}\left(xy+yz+zx\right)ds&=&\displaystyle\int_{0}^{1}t^{3}\cdot\sqrt{4t^{2}+1}dt\end{eqnarray}
ここで、\(t=\displaystyle\frac{1}{2}\tan{\theta}\) と置換すると、\(t^{3}\cdot\sqrt{4t^{2}+1}\) は
\begin{eqnarray}t^{3}\cdot\sqrt{4t^{2}+1}&=&\displaystyle\frac{1}{8}\tan^{3}{\theta}\cdot\sqrt{4\cdot\displaystyle\frac{1}{4}\tan^{2}{\theta}+1}\\\\&=&\displaystyle\frac{1}{8}\tan^{3}{\theta}\cdot\sqrt{\tan^{2}{\theta}+1}\\\\&=&\displaystyle\frac{1}{8}\tan^{3}{\theta}\cdot\sqrt{\displaystyle\frac{1}{\cos^{2}{\theta}}}\\\\&=&\displaystyle\frac{1}{8}\tan^{3}{\theta}\cdot\displaystyle\frac{1}{\cos{\theta}}\\\\&=&\displaystyle\frac{1}{8}\displaystyle\frac{\sin^{3}{\theta}}{\cos^{3}{\theta}}\cdot\displaystyle\frac{1}{\cos{\theta}}\\\\&=&\displaystyle\frac{1}{8}\displaystyle\frac{\sin^{3}{\theta}}{\cos^{4}{\theta}}\end{eqnarray}
と求まる。\(dt\) は
\begin{eqnarray}dt=\displaystyle\frac{1}{2}\displaystyle\frac{1}{\cos^{2}{\theta}}d\theta\end{eqnarray}
と求まる。\(\theta\) の積分範囲は \(t=0\) と \(t=1\) を代入して
\begin{eqnarray}0\leq t \leq 1\ \ \rightarrow\ \ 0\leq \theta \leq \alpha\ \left(\ \ \alpha\ \ は\ \ \tan{\alpha}=2\ \ を満たす定数\right)\end{eqnarray}
と求まる。これらを用いて
\begin{eqnarray}\displaystyle\int_{0}^{1}t^{3}\cdot\sqrt{4t^{2}+1}dt&=&\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{8}\displaystyle\frac{\sin^{3}{\theta}}{\cos^{4}{\theta}}\cdot\displaystyle\frac{1}{2}\displaystyle\frac{1}{\cos^{2}{\theta}}d\theta\\\\&=&\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\sin^{3}{\theta}}{\cos^{6}{\theta}}d\theta\\\\&=&\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\sin^{2}{\theta}\cdot\sin{\theta}}{\cos^{6}{\theta}}d\theta\\\\&=&\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\left(1-\cos^{2}{\theta}\right)}{\cos^{6}{\theta}}\sin{\theta}d\theta\end{eqnarray}
さらに、 \(u=\cos{\theta}\) と置くと、
\(\displaystyle\frac{\left(1-\cos^{2}{\theta}\right)}{\cos^{6}{\theta}}\) は、
\begin{eqnarray}\displaystyle\frac{\left(1-\cos^{2}{\theta}\right)}{\cos^{6}{\theta}}=\displaystyle\frac{\left(1-u^{2}\right)}{u^{6}}\end{eqnarray}
と求まる。次に、 \(du\) は
\begin{eqnarray}du&=&-\sin{\theta}d\theta\end{eqnarray}
と求まる。さらに、 \(u\) の積分範囲は
$$\cos{0}=1$$
\begin{eqnarray}\cos{\alpha}&=&\sqrt{\displaystyle\frac{1}{1+\tan^{2}{\alpha}}}\\\\&=&\sqrt{\displaystyle\frac{1}{1+2^{2}}}\\\\&=&\displaystyle\frac{1}{\sqrt{5}}\end{eqnarray}
であるので、次のように置換される。
\begin{eqnarray} 0\leq \theta \leq \alpha\ \ \rightarrow\ \ 1\leq u \leq \displaystyle\frac{1}{\sqrt{5}}\ \end{eqnarray}
改めて先ほどの積分は
\begin{eqnarray}\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\left(1-\cos^{2}{\theta}\right)}{\cos^{6}{\theta}}\sin{\theta}d\theta&=&-\displaystyle\int_{0}^{\alpha}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\left(1-\cos^{2}{\theta}\right)}{\cos^{6}{\theta}}\left(-\sin{\theta}\right)d\theta\\\\&=&-\displaystyle\int_{1}^{\frac{1}{\sqrt{5}}}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\left(1-u^{2}\right)}{u^{6}}du\\\\&=&\displaystyle\int_{\frac{1}{\sqrt{5}}}^{1}\displaystyle\frac{1}{16}\cdot\displaystyle\frac{\left(1-u^{2}\right)}{u^{6}}du\\\\&=&\displaystyle\int_{\frac{1}{\sqrt{5}}}^{1}\displaystyle\frac{1}{16}\cdot\left(u^{-6}-u^{-4}\right)du\\\\&=&\displaystyle\frac{1}{16}\left[-\displaystyle\frac{1}{5}\cdot u^{-5}+\displaystyle\frac{1}{3}\cdot u^{-3}\right]_{\frac{1}{\sqrt{5}}}^{1}\\\\&=&\displaystyle\frac{1}{16}\{\left(-\displaystyle\frac{1}{5}\cdot 1^{-5}+\displaystyle\frac{1}{3}\cdot 1^{-3}\right)-\left(-\displaystyle\frac{1}{5}\cdot\left(\displaystyle\frac{1}{\sqrt{5}}\right)^{-5}+\displaystyle\frac{1}{3}\cdot\left(\displaystyle\frac{1}{\sqrt{5}}\right)^{-3}\right)\}\\\\&=&\displaystyle\frac{1}{16}\{\displaystyle\frac{-3+5}{15}-\left(-\displaystyle\frac{1}{5}\cdot {\sqrt{5}}^{5}+\displaystyle\frac{1}{3}\cdot {\sqrt{5}}^{3}\right)\}\\\\&=&\displaystyle\frac{1}{16}\{\displaystyle\frac{2}{15}-\left(-5\cdot\sqrt{5}+\displaystyle\frac{5}{3}\cdot\sqrt{5}\right)\}\\\\&=&\displaystyle\frac{1}{16}\{\displaystyle\frac{2}{15}+\displaystyle\frac{10}{3}\sqrt{5}\}\\\\&=&\displaystyle\frac{1}{24}\left(\displaystyle\frac{1}{5}+5\sqrt{5}\right)\end{eqnarray}
$$\displaystyle\frac{1}{24}\left(\displaystyle\frac{1}{5}+5\sqrt{5}\right)$$
練習問題
原点 \(O\) から点 \(A\left(6,8,0\right)\) を通り、点 \(B\left(6,8,10\right)\) に向かう折れ線を積分経路 \(C\) とした時
スカラー関数 \(f\left(x,y,z\right)=x+y+z\) をこの経路 \(C\) に沿って線積分せよ。
まとめ
・高校数学までの積分までは \(x\) 軸に沿った積分が大半であった。
・線積分 はこの積分経路が 曲線 や 折れ線 といったように 積分経路の自由度が上がった ものである。
・ 線積分 の計算は 関数 \(f\left(x,y,z\right)\) と 線素 \(ds\) を変数 \(t\) で統一して表現することで、\(t\) のみの積分へと置き換える。