ベクトルの外積
2つのベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\)、\(\pmb{b}=\left(b_{1},b_{2},b_{3}\right)\) に対して
$$ \pmb{a}\times\pmb{b}=\begin{vmatrix} \pmb{i} & \pmb{j} & \pmb{k} \\a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\end{vmatrix}$$
をベクトル \(\pmb{a}\) と \(\pmb{b}\) の 外積 と呼ぶ。内積がスカラーを生み出していたのに対して、外積 は ベクトル を生み出す。
右辺の行列式の計算は下記事のサラスの公式を参照頂きたい。

実際に、サラスの公式を使って外積計算をもう少し計算してみると、
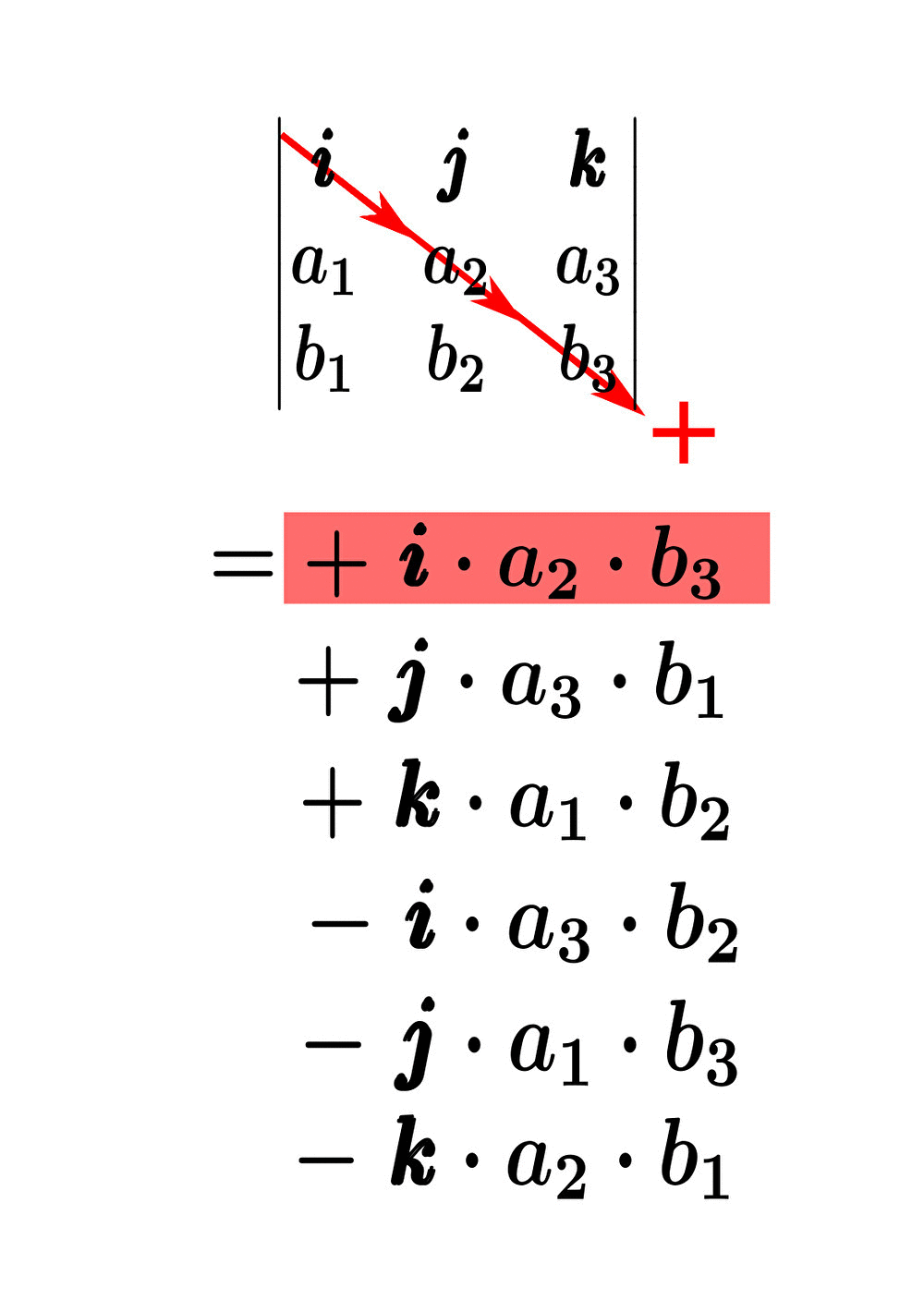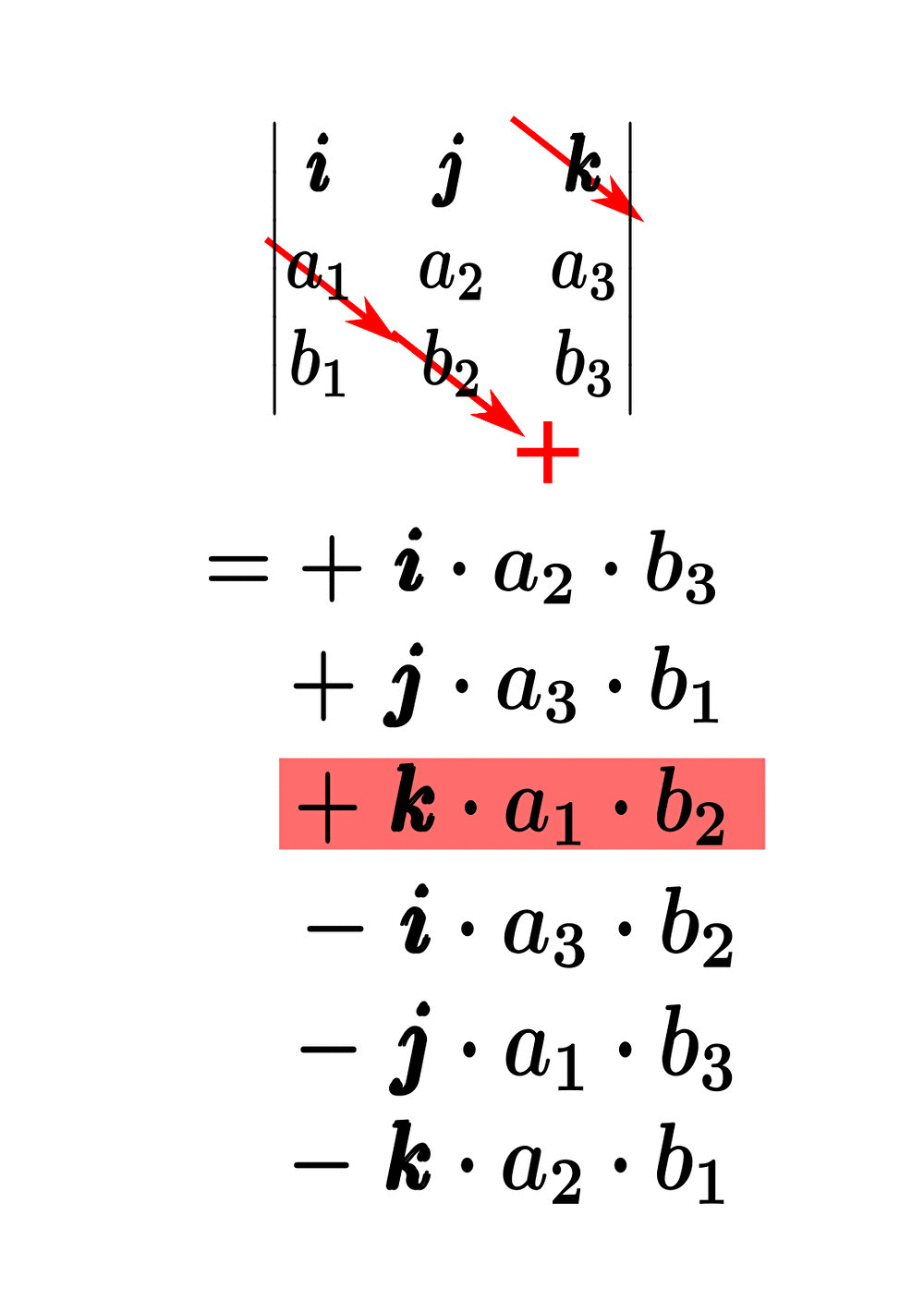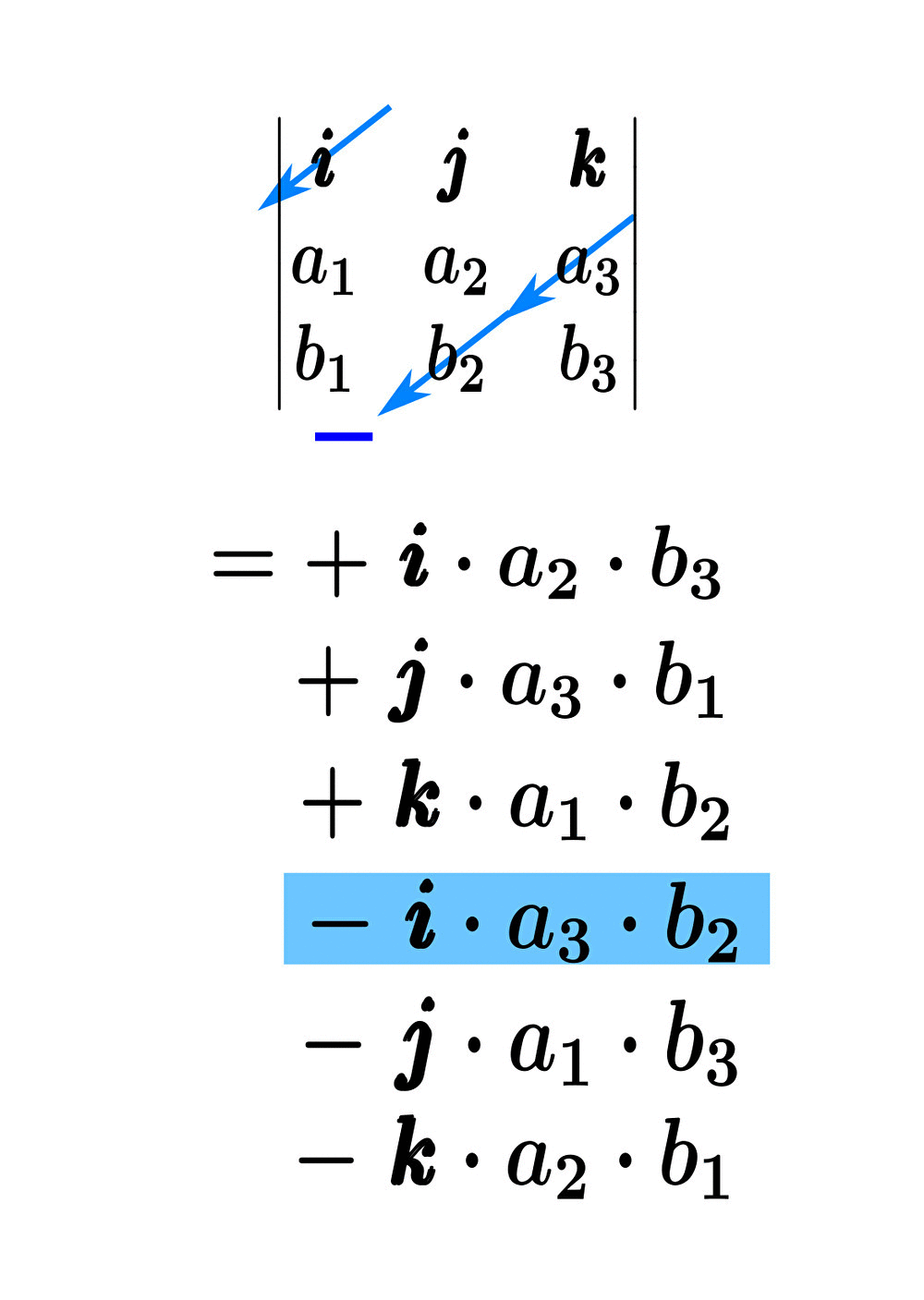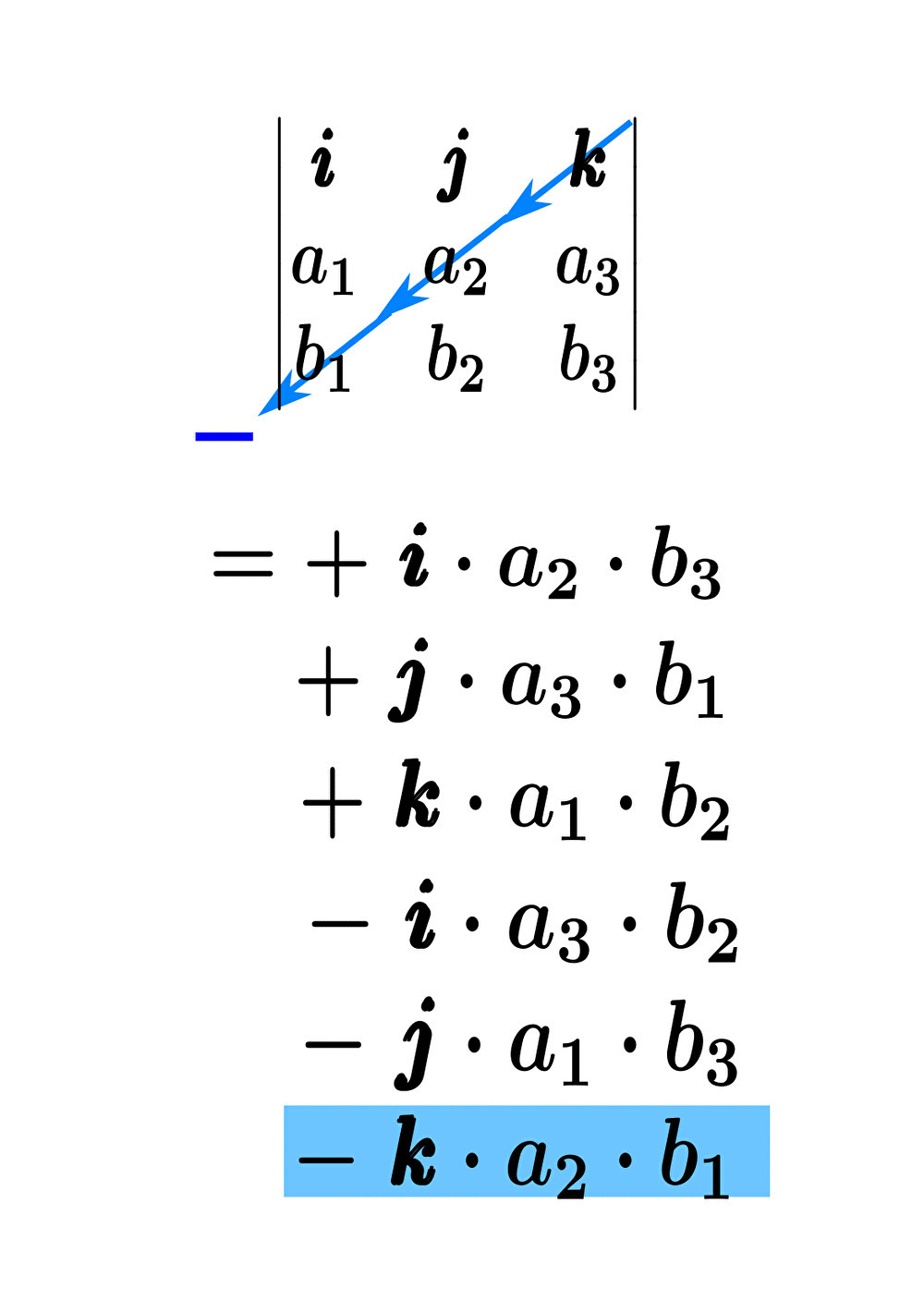
すなわち
\begin{eqnarray}&&\pmb{a}\times\pmb{b}\\\\&=&\color{red}{+\pmb{i}\cdot a_{2}\cdot b_{3}} \color{red}{ +\pmb{j}\cdot a_{3}\cdot b_{1}} \color{red}{ +\pmb{k}\cdot a_{1}\cdot b_{2}} \color{blue}{ -\pmb{i}\cdot a_{3}\cdot b_{2}} \color{blue}{ -\pmb{j}\cdot a_{1}\cdot b_{3}} \color{blue}{ -\pmb{k}\cdot a_{2}\cdot b_{1}}\\\\&=&\left(a_{2}b_{3}-a_{3}b_{2}\right)\pmb{i}+ \left(a_{3}b_{1}-a_{1}b_{3}\right)\pmb{j}+\left(a_{1}b_{2}-a_{2}b_{1}\right)\pmb{k} \end{eqnarray}
と書ける。かっこ書きで成分表示すると、
$$\pmb{a}\times\pmb{b}=\left( \ a_{2}b_{3}-a_{3}b_{2} \ , \ a_{3}b_{1}-a_{1}b_{3} \ , \ a_{1}b_{2}-a_{2}b_{1} \ \right)\cdot\cdot\cdot\left(A\right)$$
外積の計算性質
外積 は交換律は成り立たない。分配律・結合律は成り立つ。
外積 計算の主な性質は次のものがある。
- \(\color{red}{\pmb{a}}\times\color{red}{\pmb{a}}=\pmb{0}\)
- \(\color{red}{\pmb{a}}\times\color{blue}{\pmb{b}}=-\color{blue}{\pmb{b}}\times\color{red}{\pmb{a}}\)
- \(k\color{red}{\pmb{a}}\times\color{blue}{\pmb{b}}=\color{red}{\pmb{a}}\times k\color{blue}{\pmb{b}}=k\left(\color{red}{\pmb{a}}\times\color{blue}{\pmb{b}}\right)\)
- \(\color{red}{\pmb{a}}\times\left(\color{blue}{\pmb{b}}+\color{green}{\pmb{c}}\right)=\color{red}{\pmb{a}}\times\color{blue}{\pmb{b}}+\color{red}{\pmb{a}}\times\color{green}{\pmb{c}}\)
ただし、\(k\) は実数スカラー
各証明は以下の通り。
いずれも左辺を実際に 外積 計算することで右辺を導く。
先ほどの外積の計算結果(式 \(\left(A\right)\) )にて、ベクトル \(\pmb{b}\) をベクトル \(\pmb{a}\) に置き換える。すなわち、\(b_{1}\rightarrow a_{1}\)、\(b_{2}\rightarrow a_{2}\)、\(b_{3}\rightarrow a_{3}\) と置き換えると
\begin{eqnarray}\pmb{a}\times\pmb{a}&=&\left( \ a_{2}a_{3}-a_{3}a_{2} \ , \ a_{3}a_{1}-a_{1}a_{3} \ , \ a_{1}a_{2}-a_{2}a_{1} \ \right)\\\\&=& \left( 0, 0, 0\right) \\\\&=&\pmb{0}\end{eqnarray}
外積 \( \pmb{b}\times\pmb{a} \) は
\begin{eqnarray}&&\pmb{b}\times\pmb{a}\\\\&=&\left( \ b_{2}a_{3}-b_{3}a_{2} \ , \ b_{3}a_{1}-b_{1}a_{3} \ , \ b_{1}a_{2}-b_{2}a_{1} \ \right)\\\\&=& \left( \ a_{3}b_{2}- a_{2} b_{3} \ , \ a_{1}b_{3}- a_{3}b_{1} \ , \ a_{2}b_{1}- a_{1}b_{2} \ \right)\end{eqnarray}
となる。対して外積 \( \pmb{a}\times\pmb{b} \) は式 \(\left(A\right)\) から
\begin{eqnarray}&&\pmb{a}\times\pmb{b}\\\\&=&\left( \ a_{2}b_{3}-a_{3}b_{2} \ , \ a_{3}b_{1}-a_{1}b_{3} \ , \ a_{1}b_{2}-a_{2}b_{1} \ \right)\\\\&=& \left( \ -\{ a_{3}b_{2}- a_{2} b_{3}\} \ , \ -\{a_{3}b_{1}- a_{1}b_{3}\} \ , \ -\{a_{2}b_{1}- a_{1}b_{2}\} \ \right) \\\\&=&-\left( \ a_{3}b_{2}- a_{2} b_{3} \ , \ a_{1}b_{3}- a_{3}b_{1} \ , \ a_{2}b_{1}- a_{1}b_{2} \ \right)\\\\&=&- \pmb{b}\times\pmb{a} \end{eqnarray}
実際に 外積 計算して同じベクトル成分を得られるかを確認する。
まずは第1式。式 \(\left(A\right)\) のベクトル \(\pmb{a}\) を \(k\pmb{a}\) に置き換える。すなわち、\(a_{1}\rightarrow ka_{1}\)、\(a_{2}\rightarrow ka_{2}\)、\(a_{3}\rightarrow ka_{3}\) と置き換えると
\begin{eqnarray}&&k\pmb{a}\times\pmb{b}\\\\&=&\left( \ \{ka_{2}\}b_{3}-\{ka_{3}\}b_{2} \ , \ \{ka_{3}\}b_{1}-\{ka_{1}\}b_{3} \ , \ \{ka_{1}\}b_{2}-\{ka_{2}\}b_{1} \ \right)\\\\&=&\left( \ ka_{2}b_{3}-ka_{3}b_{2} \ , \ ka_{3}b_{1}-ka_{1}b_{3} \ , \ ka_{1}b_{2}-ka_{2}b_{1} \ \right)\\\\&=&k\left( \ a_{2}b_{3}-a_{3}b_{2} \ , \ a_{3}b_{1}-a_{1}b_{3} \ , \ a_{1}b_{2}-a_{2}b_{1} \ \right)\\\\&=&k\left(\pmb{a}\times\pmb{b}\right)\end{eqnarray}
次に、第2式。式 \(\left(A\right)\) のベクトル \(\pmb{b}\) を \(k\pmb{b}\) に置き換える。すなわち、\(b_{1}\rightarrow kb_{1}\)、\(b_{2}\rightarrow kb_{2}\)、\(b_{3}\rightarrow kb_{3}\) と置き換えると
\begin{eqnarray}&&\pmb{a}\times k\pmb{b}\\\\&=&\left( \ a_{2}\{kb_{3}\}-a_{3}\{kb_{2}\} \ , \ a_{3}\{kb_{1}\}-a_{1}\{kb_{3}\} \ , \ a_{1}\{kb_{2}\}-a_{2}\{kb_{1}\} \ \right)\\\\&=&\left( \ a_{2}kb_{3}-a_{3}kb_{2} \ , \ a_{3}kb_{1}-a_{1}kb_{3} \ , \ a_{1}kb_{2}-a_{2}kb_{1} \ \right)\\\\&=&\left( \ ka_{2}b_{3}-ka_{3}b_{2} \ , \ ka_{3}b_{1}-ka_{1}b_{3} \ , \ ka_{1}b_{2}-ka_{2}b_{1} \ \right)\\\\&=&k\left( \ a_{2}b_{3}-a_{3}b_{2} \ , \ a_{3}b_{1}-a_{1}b_{3} \ , \ a_{1}b_{2}-a_{2}b_{1} \ \right)\\\\&=&k\left(\pmb{a}\times\pmb{b}\right)\end{eqnarray}
この2式を繋げて
$$ k\pmb{a}\times\pmb{b}= \pmb{a}\times k\pmb{b}=k\left(\pmb{a}\times\pmb{b}\right) $$
左辺を実際に 外積 計算してみる。
式 \(\left(A\right)\) のベクトル \(\pmb{b}\) を \(\pmb{b}+\pmb{c}\) に置き換える。すなわち、\(b_{1}\rightarrow b_{1}+c_{1}\)、\(b_{2}\rightarrow b_{2}+c_{2}\)、\(b_{3}\rightarrow b_{3}+c_{3}\) と置き換える。
今回は、式が長くなるので見やすさ向上のため 基本ベクトル を用いた成分表示を行った。
\begin{eqnarray}&&\pmb{a}\times \left(\pmb{b}+ \pmb{c} \right)\\\\ &=&\{a_{2}\left(b_{3}+c_{3}\right)-a_{3}\left(b_{2}+c_{2}\right)\}\pmb{i}+\{a_{3}\left(b_{1}+c_{1}\right)-a_{1}\left(b_{3} +c_{3}\right)\}\pmb{j}+\{a_{1}\left( b_{2}+c_{2}\right)-a_{2}\left( b_{1}+c_{1}\right)\}\pmb{k}\\\\&=&\{a_{2}b_{3}+a_{2}c_{3}-a_{3}b_{2}+a_{3}c_{2}\}\pmb{i}+\{a_{3}b_{1}+a_{3}c_{1}-a_{1}b_{3} +a_{1}c_{3}\}\pmb{j}+\{a_{1}b_{2}+a_{1}c_{2}-a_{2}b_{1}+a_{2}c_{1}\}\pmb{k}\\\\&=&\{\left(a_{2}b_{3}-a_{3}b_{2}\right)+\left(a_{2}c_{3}-a_{3}c_{2}\right)\}\pmb{i}+\{\left(a_{3}b_{1}-a_{1}b_{3}\right)+\left(a_{3}c_{1}-a_{1}c_{3}\right)\}\pmb{j}+\{\left( a_{1}b_{2}-a_{2}b_{1}\right)+\left( a_{1}c_{2}-a_{2}c_{1}\right)\}\pmb{k}\\\\&=&\left[\left(a_{2}b_{3}-a_{3}b_{2}\right)\pmb{i}+\left(a_{3}b_{1}-a_{1}b_{3}\right)\pmb{j}+\left( a_{1}b_{2}-a_{2}b_{1}\right)\pmb{k}\right]+\left[\left(a_{2}c_{3}-a_{3}c_{2}\right)\pmb{i}+\left(a_{3}c_{1}-a_{1}c_{3}\right)\pmb{j}+\left( a_{1}c_{2}-a_{2}c_{1}\right)\pmb{k}\right]\\\\&=&\left( \ a_{2}b_{3}-a_{3}b_{2} \ , \ a_{3}b_{1}-a_{1}b_{3} \ , \ a_{1}b_{2}-a_{2}b_{1} \ \right)+\left( \ a_{2}c_{3}-a_{3}c_{2} \ , \ a_{3}c_{1}-a_{1}c_{3} \ , \ a_{1}c_{2}-a_{2}c_{1} \ \right)\\\\&=&\pmb{a}\times \pmb{b}+\pmb{a}\times \pmb{c}\end{eqnarray}
基本ベクトル \(\pmb{i}=\left(1,0,0\right)\)、\(\pmb{j}=\left(0,1,0\right)\)、\(\pmb{k}=\left(0,0,1\right)\) どうしの 外積 を求めてみよう。
外積の計算性質①より、自分同士の 外積 は \(0\) ベクトルなので
$$\pmb{i}\times\pmb{i}=\pmb{j}\times\pmb{j}=\pmb{k}\times\pmb{k}=\pmb{0}$$
となる。
次に、異なる2つの基本ベクトル同士の 外積 を求めてみよう。
\begin{eqnarray}&&\pmb{i}\times\pmb{j}\\\\&=&\begin{vmatrix} \pmb{i} & \pmb{j} & \pmb{k} \\1 & 0 & 0\\0 & 1 & 0\end{vmatrix}\\\\&=&\left(0\times 0-0\times 1\right)\pmb{i}+ \left(0\times 0-1\times 0\right)\pmb{j}+\left(1\times 1-0\times 0\right)\pmb{k}\\\\&=&\pmb{k}\end{eqnarray}
\begin{eqnarray}&&\pmb{j}\times\pmb{k}\\\\&=&\begin{vmatrix} \pmb{i} & \pmb{j} & \pmb{k} \\0 & 1 & 0\\0 & 0 & 1\end{vmatrix}\\\\&=&\left(1\times 1-0\times 0\right)\pmb{i}+ \left(0\times 0-0\times 1\right)\pmb{j}+\left(0\times 0-1\times 0\right)\pmb{k}\\\\&=&\pmb{i}\end{eqnarray}
\begin{eqnarray}&&\pmb{j}\times\pmb{k}\\\\&=&\begin{vmatrix} \pmb{i} & \pmb{j} & \pmb{k} \\0 & 1 & 0\\0 & 0 & 1\end{vmatrix}\\\\&=&\left(1\times 1-0\times 0\right)\pmb{i}+ \left(0\times 0-0\times 1\right)\pmb{j}+\left(0\times 0-1\times 0\right)\pmb{k}\\\\&=&\pmb{i}\end{eqnarray}
このように、異なる2つの 基本ベクトル どうしの 外積 は計算に参加していない3つ目の基本ベクトルとなる。
外積の図形的意味
端的に言えば、外積は「2つのベクトルからそれらと垂直なベクトルを作る」意味合いを持つ。
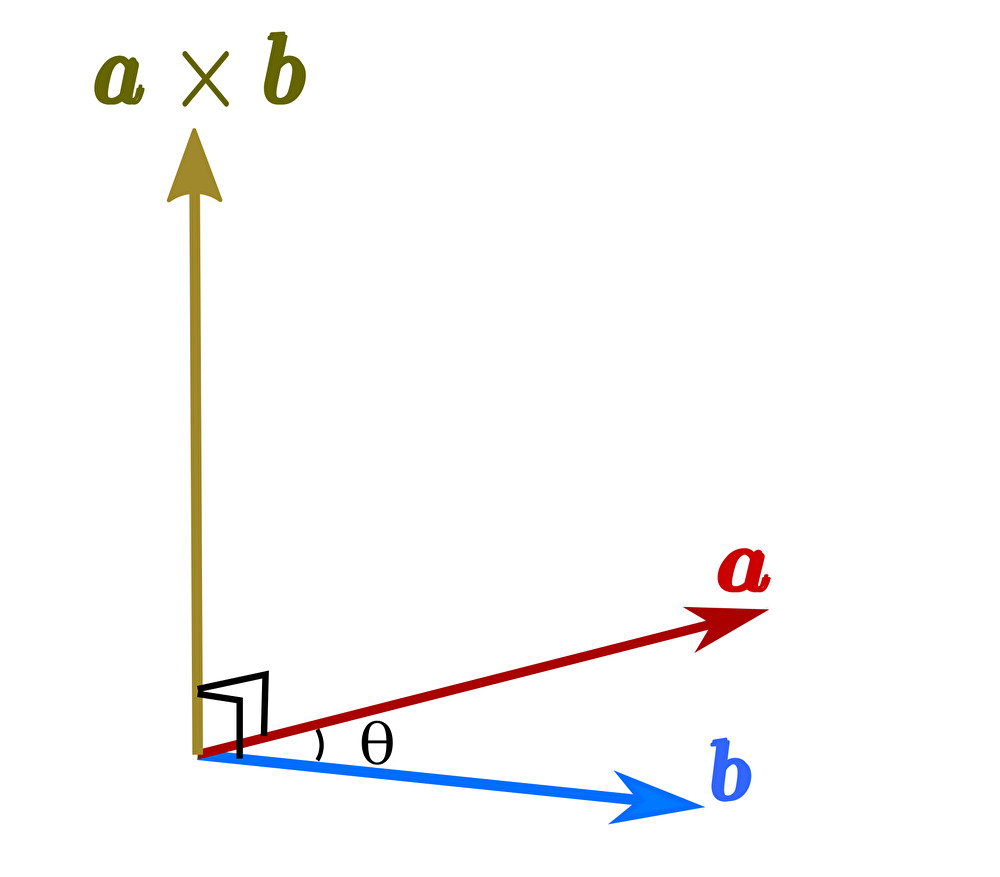
また、ベクトル \(\pmb{a}\) と \(\pmb{b}\) のなす角を \(\theta\) とすると、外積は次のようにも表現される。
$$ |\pmb{a}\times \pmb{b}|=| \pmb{a} || \pmb{b} |\sin{\theta}$$
内積とは違い サイン で定義されている。
外積があって嬉しいこと
中学校の理科で次の図を見たことがある人も多いのではないだろうか。
-1024x686.png)
緑の棒には電流が流れている。
さて、磁界は電流の流れている物体に対して力を発生させる。その力の向きはどの方向だろうか。
磁界の向き、電流の向きが分かっているので、力の向きは「フレミングの左手の法則」より次のように求まる。
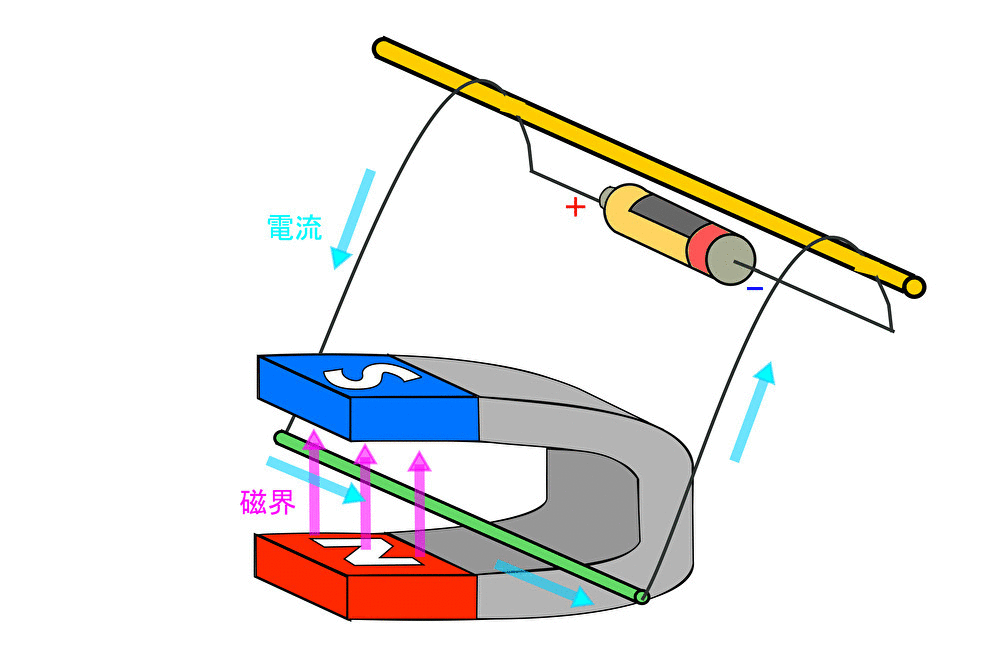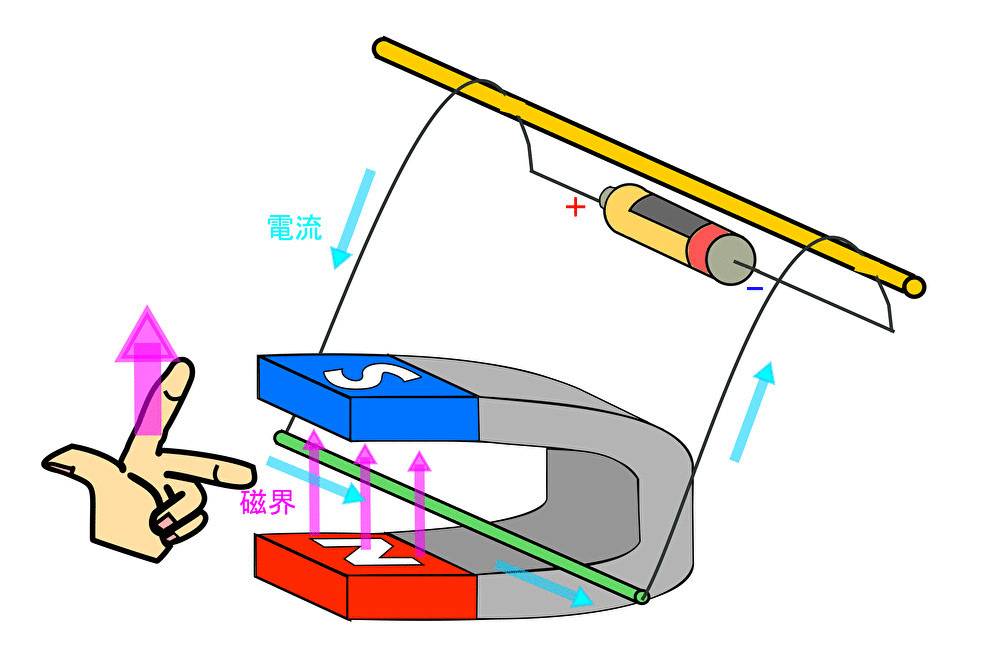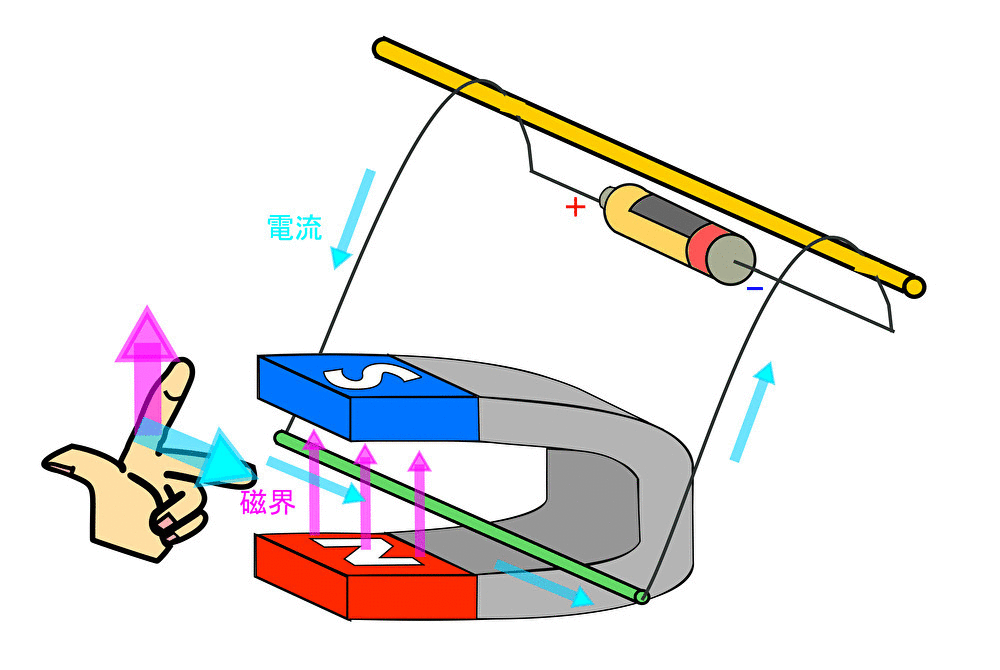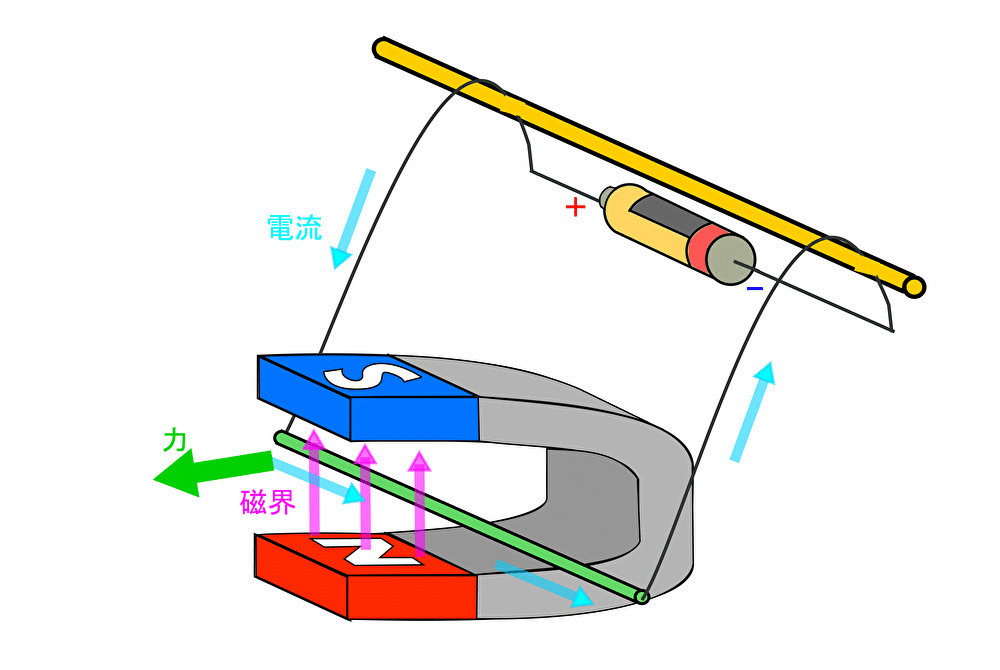
力の向き は親指の方向で示された。
この例のように、2つのベクトル(例で言う 磁界、電流)から新たなベクトル(力)を求めることは物理の世界ではちょいちょいある。
この「2個のベクトルから1個のベクトルを作る」ことを計算で示して、式で表現できるようにしたものこそが 外積 である。
外積で表現することによって、成分計算で解析的に力のベクトルなどを求められるようになる。
例題
あるベクトル \(\pmb{a}\) について
$$\left(\pmb{i}\cdot\pmb{a}\right)\left(\pmb{i}\times\pmb{a}\right)+\left(\pmb{j}\cdot\pmb{a}\right)\left(\pmb{j}\times\pmb{a}\right)+\left(\pmb{k}\cdot\pmb{a}\right)\left(\pmb{k}\times\pmb{a}\right)=\pmb{0}$$
が成り立つことを示せ。
例題の解答
各項を地道に成分計算する。
ベクトル \(\pmb{a}\) の成分を \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) とすると
まずは第1項について
\begin{eqnarray}\pmb{i}\cdot\pmb{a}&=&\left(1,0,0\right)\cdot\left(a_{1},a_{2},a_{3}\right)\\\\&=&1\times a_{1}+0\times a_{2}+0\times a_{3}\\\\&=&a_{1}\end{eqnarray}
\begin{eqnarray}&&\pmb{i}\times\pmb{a}\\\\&=&\begin{vmatrix} \pmb{i} & \pmb{j} & \pmb{k}\\ 1 & 0 & 0 \\a_{1} & a_{2} & a_{3}\end{vmatrix}\\\\&=&\left(0\times a_{3}-0\times a_{2}\right)\pmb{i}+ \left(0\times a_{1}-1\times a_{3}\right)\pmb{j}+\left(1\times a_{2}-0\times a_{1}\right)\pmb{k}\\\\&=&-a_{3}\pmb{j}+a_{2}\pmb{k}\end{eqnarray}
従って、
\begin{eqnarray} &&\left(\pmb{i}\cdot\pmb{a}\right)\left(\pmb{i}\times\pmb{a}\right)\\\\&=& a_{1}\left( -a_{3}\pmb{j}+a_{2}\pmb{k} \right)\\\\&=& – a_{1}a_{3}\pmb{j}+ a_{1}a_{2}\pmb{k} \end{eqnarray}
第2項、第3項についても同様に計算して
\begin{eqnarray} &&\left(\pmb{j}\cdot\pmb{a}\right)\left(\pmb{j}\times\pmb{a}\right)\\\\&=& a_{2}\left( -a_{1}\pmb{k}+a_{3}\pmb{i} \right)\\\\&=& a_{2}a_{3}\pmb{i}- a_{2}a_{1}\pmb{k} \end{eqnarray}
\begin{eqnarray} &&\left(\pmb{k}\cdot\pmb{a}\right)\left(\pmb{k}\times\pmb{a}\right)\\\\&=& a_{3}\left( -a_{2}\pmb{i}+a_{1}\pmb{j} \right)\\\\&=& – a_{3}a_{2}\pmb{i}+ a_{3}a_{1}\pmb{j} \end{eqnarray}
これらを足し合わせて
\begin{eqnarray}&&\left(\pmb{i}\cdot\pmb{a}\right)\left(\pmb{i}\times\pmb{a}\right)+\left(\pmb{j}\cdot\pmb{a}\right)\left(\pmb{j}\times\pmb{a}\right)+\left(\pmb{k}\cdot\pmb{a}\right)\left(\pmb{k}\times\pmb{a}\right)\\\\&=&- a_{1}a_{3}\pmb{j}+ a_{1}a_{2}\pmb{k}+a_{2}a_{3}\pmb{i}- a_{1}a_{2}\pmb{k}- a_{3}a_{2}\pmb{i}+ a_{3}a_{1}\pmb{j}\\\\&=&\left(a_{2}a_{3}-a_{3}a_{2}\right)\pmb{i}+\left(a_{1}a_{3}-a_{3}a_{1}\right)\pmb{j}+\left(a_{1}a_{2}-a_{2}a_{1}\right)\pmb{k}\\\\&=&0\pmb{i}+0\pmb{j}+0\pmb{k}\\\\&=&\pmb{0}\end{eqnarray}
まとめ
・外積は \(3\times 3\) 行列式で計算する。
・外積は2つのベクトルからそれらと 垂直なベクトルを作る 意味合いを持つ。