ベクトルの内積
2つのベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) と \(\pmb{b}=\left(b_{1},b_{2},b_{3}\right)\) について、各成分の積の和 \(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\) を
ベクトル \(\pmb{a}\) と \(\pmb{b}\) の 内積 と呼び、\(\pmb{a}\cdot\pmb{b}\) と書く。
つまり
$$\pmb{a}\cdot\pmb{b}= a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} $$
と書く。 内積 は成分(数字)の積の和であるので スカラー である。
内積は数字どうしの掛け算と同様に、次の 交換律、分配律、結合律 が成り立つ。
- \( \color{red}{\pmb{a}}\cdot\color{blue}{\pmb{b}}= \color{blue} {\pmb{b}}\cdot \color{red}{\pmb{a}}\\ \)
- \( \color{red}{\pmb{a}}\cdot\left( \color{blue}{ \pmb{b}}+ \color{green}{\pmb{c}}\right)= \color{red}{\pmb{a}} \cdot \color{blue}{ \pmb{b}} + \color{red}{\pmb{a}} \cdot \color{green}{\pmb{c}} \\ \left( \color{red}{\pmb{a}} + \color{blue}{ \pmb{b}} \right) \cdot \color{green}{\pmb{c}} = \color{red}{\pmb{a}} \cdot \color{green}{\pmb{c}} + \color{blue}{ \pmb{b}} \cdot \color{green}{\pmb{c}} \\\)
- \(\left(k \pmb{a} \right)\cdot\pmb{b}= \pmb{a} \cdot \left(k \pmb{b} \right) =k \left( \pmb{a} \cdot \pmb{b} \right) \)
ただし、\(k\) は実数スカラー
基本ベクトル \(\pmb{i}=\left(1,0,0\right)\)、\(\pmb{j}=\left(0,1,0\right)\)、\(\pmb{k}=\left(0,0,1\right)\) について総当たりで 内積 をとると、
\begin{cases}\pmb{i}\cdot\pmb{i}=\left(1,0,0\right)\cdot\left(1,0,0\right)=1\times 1+0\times 0+0\times 0=1\\\\\pmb{j}\cdot\pmb{j}=\left(0,1,0\right)\cdot\left(0,1,0\right)=0\times 0+1\times 1+0\times 0=1\\\\\pmb{k}\cdot\pmb{k}=\left(0,0,1\right)\cdot\left(0,0,1\right)=0\times 0+0\times 0+1\times 1=1\end{cases}
\begin{cases}\pmb{i}\cdot\pmb{j}=\left(1,0,0\right)\cdot\left(0,1,0\right)=1\times 0+0\times 1+0\times 0=0\\\\\pmb{j}\cdot\pmb{k}=\left(0,1,0\right)\cdot\left(0,0,1\right)=0\times 0+1\times 0+0\times 1=0\\\\\pmb{k}\cdot\pmb{i}=\left(0,0,1\right)\cdot\left(1,0,0\right)=0\times 1+0\times 0+1\times 0=0\end{cases}
すなわち
$$ \pmb{i}\cdot\pmb{i} = \pmb{j}\cdot\pmb{j} = \pmb{k}\cdot\pmb{k} =1$$
$$ \pmb{i}\cdot\pmb{j} = \pmb{j}\cdot\pmb{k} = \pmb{k}\cdot\pmb{i} =0$$
基本ベクトル どうしの 内積 は「自分同士」は \(1\)、「異なる二つ」は \(0\) となることがわかる。
さて、2つのベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) と \(\pmb{b}=\left(b_{1},b_{2},b_{3}\right)\) は 基本ベクトル を用いて
\begin{cases} \pmb{a}=a_{1}\pmb{i}+ a_{2} \pmb{j}+a_{3}\pmb{k} \\\\ \pmb{b}=b_{1}\pmb{i}+ b_{2} \pmb{j}+b_{3}\pmb{k} \end{cases}
と成分表示できる。改めて2つのベクトル \(\pmb{a}\) と \(\pmb{b}\) の 内積 をとってみよう。
\begin{eqnarray} &&\pmb{a}\cdot \pmb{b}\\\\&=& \left( \color{red}{a_{1}\pmb{i}}+ \color{red}{ a_{2} \pmb{j}}+ \color{red}{ a_{3}\pmb{k} }\right)\cdot\left( \color{blue}{ b_{1}\pmb{i}}+ \color{blue}{ b_{2} \pmb{j}}+ \color{blue}{ b_{3}\pmb{k}} \right)\\\\&=& \color{red}{ a_{1}\pmb{i}} \cdot\left( \color{blue}{ b_{1}\pmb{i}}+ \color{blue}{ b_{2} \pmb{j}}+ \color{blue}{ b_{3}\pmb{k}} \right) + \color{red}{ a_{2} \pmb{j} }\cdot\left( \color{blue}{ b_{1}\pmb{i}}+ \color{blue}{ b_{2} \pmb{j}}+ \color{blue}{ b_{3}\pmb{k}} \right) + \color{red}{ a_{3}\pmb{k}} \cdot\left( \color{blue}{ b_{1}\pmb{i}}+ \color{blue}{ b_{2} \pmb{j}}+ \color{blue}{ b_{3}\pmb{k}} \right) \\\\&=&\color{red}{a_{1}}\color{blue}{b_{1}}\left(\color{red}{\pmb{i}}\cdot \color{blue}{ \pmb{i}}\right) + \color{red}{a_{1}}\color{blue}{b_{2}}\left(\color{red}{\pmb{i}}\cdot \color{blue}{ \pmb{j}}\right) + \color{red}{a_{1}}\color{blue}{b_{3}}\left(\color{red}{\pmb{i}}\cdot \color{blue}{ \pmb{k}}\right)+ \color{red}{a_{2}}\color{blue}{b_{1}}\left(\color{red}{\pmb{j}}\cdot \color{blue}{ \pmb{i}}\right)+ \color{red}{a_{2}}\color{blue}{b_{2}}\left(\color{red}{\pmb{j}}\cdot \color{blue}{ \pmb{j}}\right)+ \color{red}{a_{2}}\color{blue}{b_{3}}\left(\color{red}{\pmb{j}}\cdot \color{blue}{ \pmb{k}}\right)+ \color{red}{a_{3}}\color{blue}{b_{1}}\left(\color{red}{\pmb{k}}\cdot \color{blue}{ \pmb{i}}\right)+ \color{red}{a_{3}}\color{blue}{b_{2}}\left(\color{red}{\pmb{k}}\cdot \color{blue}{ \pmb{j}}\right) + \color{red}{a_{3}}\color{blue}{b_{3}}\left(\color{red}{\pmb{k}}\cdot \color{blue}{ \pmb{k}}\right) \end{eqnarray}
先ほど述べたように 基本ベクトル どうしの 内積 は「自分同士」は \(1\)、「異なる二つ」は \(0\) となるので
\begin{eqnarray}&&\pmb{a}\cdot \pmb{b}\\\\&=& \color{red}{a_{1}}\color{blue}{b_{1}}\times 1 + \color{red}{a_{1}}\color{blue}{b_{2}}\times 0 + \color{red}{a_{1}}\color{blue}{b_{3}}\times 0+ \color{red}{a_{2}}\color{blue}{b_{1}}\times 0+ \color{red}{a_{2}}\color{blue}{b_{2}}\times1+ \color{red}{a_{2}}\color{blue}{b_{3}}\times0+ \color{red}{a_{3}}\color{blue}{b_{1}}\times 0+ \color{red}{a_{3}}\color{blue}{b_{2}}\times 0 + \color{red}{a_{3}}\color{blue}{b_{3}}\times 1\\\\&=& \color{red}{a_{1}}\color{blue}{b_{1}}+ \color{red}{a_{2}}\color{blue}{b_{2}} + \color{red}{a_{3}}\color{blue}{b_{3}} \end{eqnarray}
となり、基本ベクトル でベクトルを成分表示した場合でも初めに述べた 内積 と同じ結果が得られる。
内積の図形的な意味
高校数学にて 内積 は次のように定義されていた。
ベクトル \(\pmb{a}\) と \(\pmb{b}\) のなす角を \(\theta\) とすると
$$ \pmb{a}\cdot\pmb{b}= |\pmb{a} || \pmb{b}|\cos{\theta} $$
この式に内積の図形的意味が含まれている。
例としてある物体を 力 \(F[N]\) で 距離 \(x[m]\) だけ動かしたときの 仕事 \(W[J]\) を考えてみよう。摩擦は考えない。
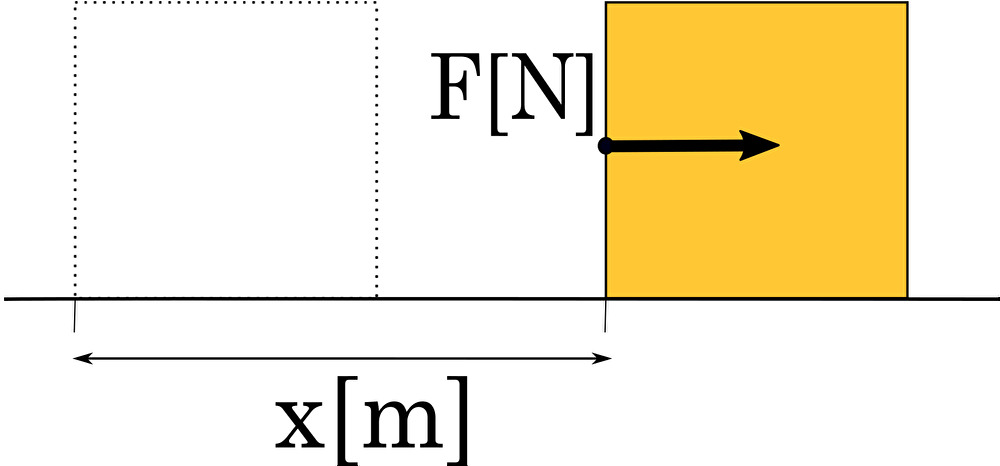
仕事 は物体に「加えた力」と物体を「動かした距離」の 積 であるので
$$W=Fx$$
と求まる。
次に、角度 \(\theta[\mathrm{rad}]\) の斜面において物体を 力 \(F[N]\) で 距離 \(x[m]\) だけ(登り方向に)動かしたときの 仕事 \(W[J]\) を考えてみよう。摩擦は考えない。
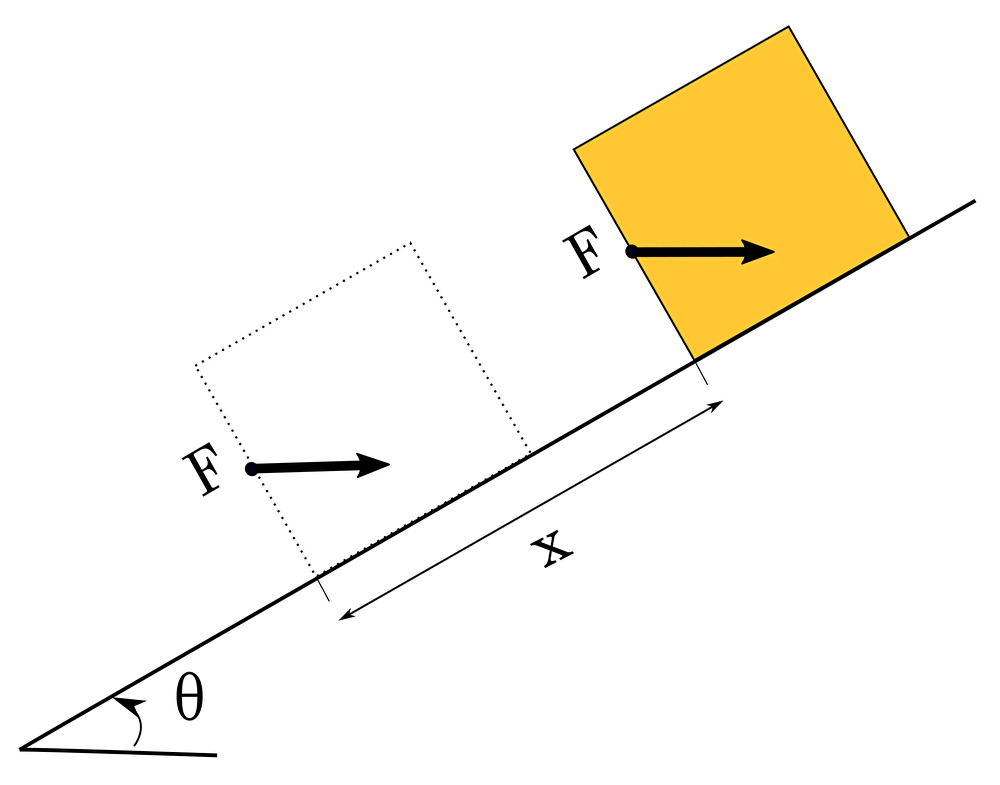
高校物理の定番問題である。さて仕事 \(W[J]\) を求めるが、先ほどと違い力のベクトル \(\vec{F}\) と押す方向のベクトル \(\vec{x}\) は同じ向きでない。(平行でない。)
仕事について、 \(F\) の 斜面方向成分 \(F\cos{\theta}\) の力で物体を斜面登り方向に距離 \(x\) だけ動かしたと考える。
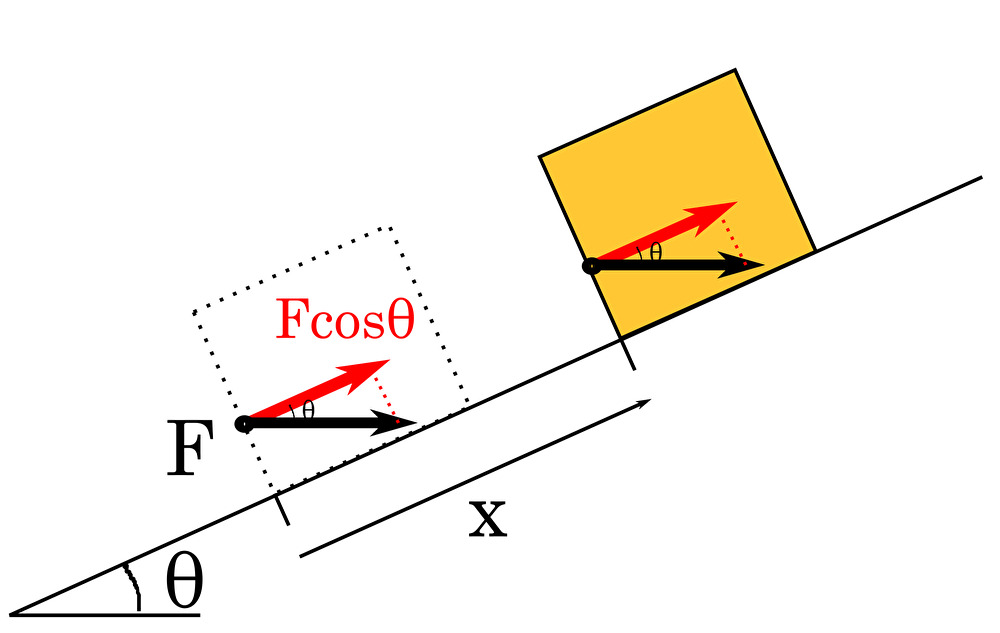
\begin{eqnarray}W&=&F\cos{\theta}\cdot x\\\\ &=&Fx\cos{\theta}\end{eqnarray}
\(F=|\vec{F}|\)、\(x=|\vec{x}|\) であるので、力・距離のベクトル \(\vec{F}\) と \(\vec{x}\) を用いて仕事の式を書き直すと
$$W= |\vec{F}| |\vec{x}| \cos{\theta} $$
右辺は見るからに「内積」の形であるので
$$W= \vec{F}\cdot\vec{x}$$
と書き直すことができる。
このように内積は図形的には ベクトルの向き合わせ の意味合いが強い。
方向余弦
突然だがベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) と 基本ベクトル \(\pmb{i}\)、 \(\pmb{j}\)、 \(\pmb{k}\) との 内積 を考えてみよう。
ベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) が \(x\) 軸、\(y\) 軸、\(z\) 軸となす角を \(\alpha\)、\(\beta\)、\(\gamma\) とする。
基本ベクトル \(\pmb{i}\)、 \(\pmb{j}\)、 \(\pmb{k}\) は \(x\) 軸、\(y\) 軸、\(z\) 軸方向の単位ベクトルであるので、ベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) と各基本ベクトルが なす角 もまた \(\alpha\)、\(\beta\)、\(\gamma\) となる。
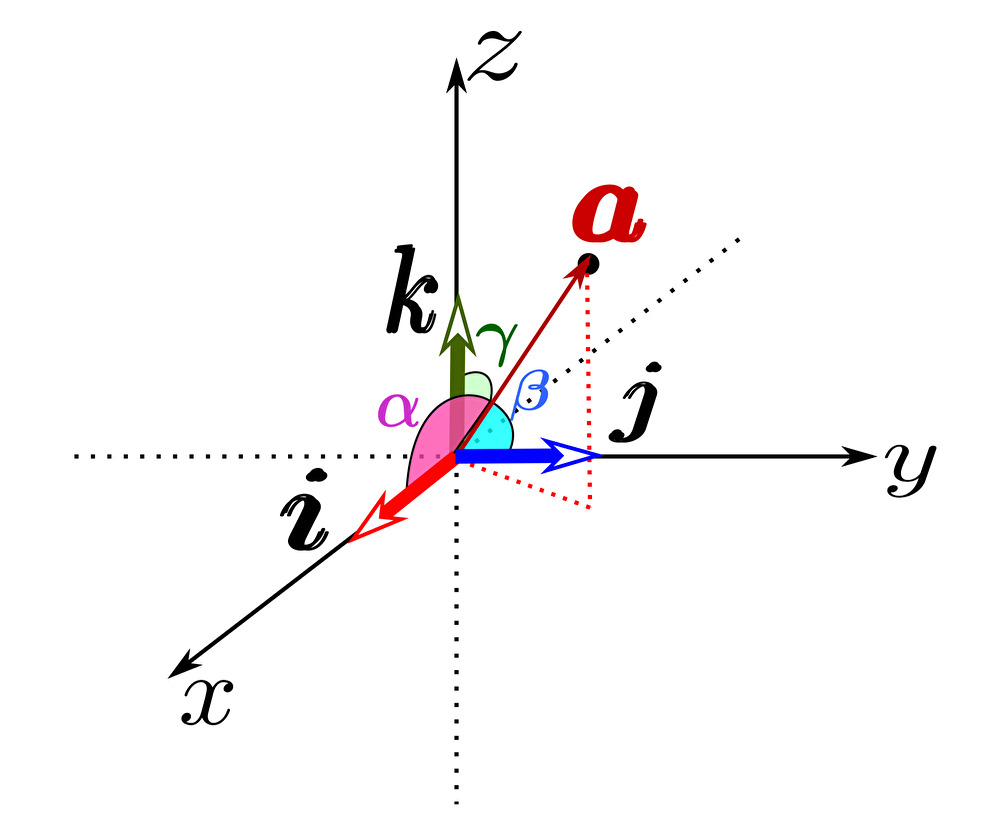
まずはベクトル \(\pmb{a}=\left(a_{1},a_{2},a_{3}\right)\) と 基本ベクトル \(\pmb{i}=\left(1,0,0\right)\) の 内積 を求めよう。成分どうしの積の和を計算して
$$ \pmb{a}\cdot \pmb{i} =a_{1}\times 1+a_{2}\times 0+a_{3}\times 0=a_{1}\cdot\cdot\cdot\left(A\right)$$
となり、ベクトル \(\pmb{a}\) の \(x\) 成分が抽出される。
$$ \pmb{a}\cdot \pmb{j} =a_{1}\times 0+a_{2}\times 1+a_{3}\times 0=a_{2}$$
となり、ベクトル \(\pmb{a}\) の \(y\) 成分が抽出される。
$$ \pmb{a}\cdot \pmb{k} =a_{1}\times 0+a_{2}\times 0+a_{3}\times 1=a_{3}$$
となり、ベクトル \(\pmb{a}\) の \(z\) 成分が抽出される。
また、ベクトル \(\pmb{a}\) と 基本ベクトル \(\pmb{i}\) の 内積 はなす角が \(\alpha\) であることに注意して次のように コサイン を用いて書ける。
$$ \pmb{a}\cdot \pmb{i} =|\pmb{a}||\pmb{i}|\cos{\alpha}= |\pmb{a}|\cos{\alpha} \cdot\cdot\cdot\left(B\right) $$
$$ \pmb{a}\cdot \pmb{j} =|\pmb{a}||\pmb{j}|\cos{\beta}= |\pmb{a}|\cos{\beta}$$
$$ \pmb{a}\cdot \pmb{k} =|\pmb{a}||\pmb{k}|\cos{\gamma}= |\pmb{a}|\cos{\gamma}$$
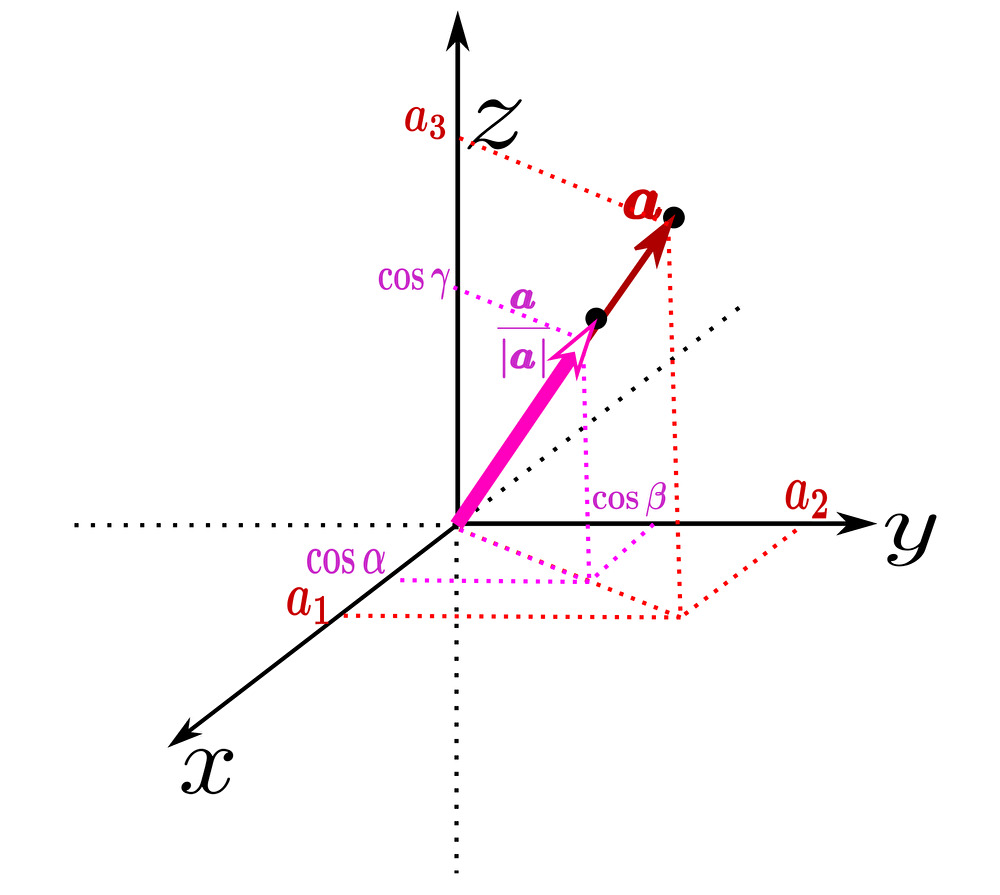
この 基本ベクトル との内積で生じた コサイン \(\left(\ \cos{\alpha},\ \cos{\beta},\ \cos{\gamma}\right)\) を 方向余弦 と呼ぶ。
式 \(\left(A\right)\) と式 \(\left(B\right)\) から右辺同士を比較して
$$ a_{1}= |\pmb{a}|\cos{\alpha} $$
$$\cos{\alpha}=\displaystyle\frac{a_{1}}{ |\pmb{a}| }\left(=\displaystyle\frac{a_{1}}{ \sqrt{a^{2}_{1}+a^{2}_{2}+a^{2}_{3}} } \right)$$
同様の計算で \(\cos{\beta}\)、\(\cos{\gamma}\) についても
$$\cos{\beta}=\displaystyle\frac{a_{2}}{ |\pmb{a}| }\left(=\displaystyle\frac{a_{2}}{ \sqrt{a^{2}_{1}+a^{2}_{2}+a^{2}_{3}} } \right)$$
$$\cos{\gamma}=\displaystyle\frac{a_{3}}{ |\pmb{a}| }\left(=\displaystyle\frac{a_{3}}{ \sqrt{a^{2}_{1}+a^{2}_{2}+a^{2}_{3}} } \right)$$
と求まる。
さて、突然だが高校数学におけるベクトル \(\pmb{a}\) の大きさを \(1\) にする計算(つまり 単位ベクトル化 )を皆さん覚えているだろうか。
そう。ベクトル \(\pmb{a}\) を自身の大きさ \(|\pmb{a}|\) で割るのである。
\begin{eqnarray}&&\displaystyle\frac{\pmb{a}}{|\pmb{a}|}\\\\&=& \displaystyle\frac{1}{|\pmb{a}|} \left(a_{1},a_{2},a_{3}\right)\\\\ &=& \left(\displaystyle\frac{a_{1}}{|\pmb{a}|} , \displaystyle\frac{a_{2}}{|\pmb{a}|} , \displaystyle\frac{a_{3}}{|\pmb{a}|} \right) \end{eqnarray}
このベクトル \(\pmb{a}\) の 単位ベクトル \(\displaystyle\frac{\pmb{a}}{|\pmb{a}|}\) の成分は先ほど求めた 方向余弦(コサイン) そのものである。
つまり
$$\displaystyle\frac{\pmb{a}}{|\pmb{a}|}=\left(\cos{\alpha} , \cos{\beta} , \cos{\gamma}\right)$$
となる。
すなわち 方向余弦 はベクトル \(\pmb{a}\) の 単位ベクトル の各成分を意味する。
例題
\(\pmb{a}=\pmb{i}-3\pmb{j}+2\pmb{k}\) の方向余弦を求めよ。
例題の解答
ベクトル \(\pmb{a}\) の \(x\) 成分、\(y\) 成分、\(z\) 成分はそれぞれ \(1\)、 \(-3\)、 \(2\) であるので
ベクトル \(\pmb{a}\) の大きさは
$$|\pmb{a}|=\sqrt{1^{2}+\left(-3\right)^{2}+2^{2}}=\sqrt{14}$$
ベクトル \(\pmb{a}\) を自身の大きさ \(|\pmb{a}|=\sqrt{14}\) で割る( 単位ベクトル化 する)と、
\begin{eqnarray}&&\displaystyle\frac{\pmb{a}}{|\pmb{a}|}\\\\&=& \displaystyle\frac{1}{|\pmb{a}|} \left( \pmb{i}-3\pmb{j}+2\pmb{k} \right)\\\\ &=& \left(\displaystyle\frac{ \pmb{i} }{|\pmb{a}|}+\displaystyle\frac{-3\pmb{j}}{|\pmb{a}|}+\displaystyle\frac{2\pmb{k}}{|\pmb{a}|}\right)\\\\ &=& \left(\displaystyle\frac{ \pmb{i} }{ \sqrt{14} }+\displaystyle\frac{-3\pmb{j}}{ \sqrt{14} }+\displaystyle\frac{2\pmb{k}}{ \sqrt{14} }\right) \\\\ &=& \left(\displaystyle\frac{1}{ \sqrt{14} } \pmb{i} -\displaystyle\frac{3}{ \sqrt{14} } \pmb{j} +\displaystyle\frac{2}{ \sqrt{14} } \pmb{k} \right) \end{eqnarray}
よって、ベクトル \(\pmb{a}\) の 単位ベクトル の成分はそれぞれ \(\displaystyle\frac{1}{ \sqrt{14} }\)、\(-\displaystyle\frac{3}{ \sqrt{14} }\)、\(\displaystyle\frac{2}{ \sqrt{14} }\) であり、これらこそが求める 方向余弦 である。
\(\displaystyle\frac{1}{ \sqrt{14} }\)、\(-\displaystyle\frac{3}{ \sqrt{14} }\)、\(\displaystyle\frac{2}{ \sqrt{14} }\)
まとめ
・ 内積 は スカラー であり、仕事・エネルギーを求める際に使うことが多い。
・ 方向余弦 は大きさが \(1\) の方向ベクトルの成分である。