スカラー場とベクトル場
ある点Pにスカラーが対応しているような空間を スカラー場 と呼び、対してある点Pにベクトルが対応しているような空間を ベクトル場 と呼ぶ。
この2つの場の違いは 向きの概念の有無 である。
例えば、温度に注目した地球という空間は スカラー場 といえる。

上の図のように地球を温度という変数で着目したとき 点B には 2.8、点L には 17.3、点Mには 6.5 という数字(スカラー)が対応している。
一方、水の流れる速度に注目した川という空間は ベクトル場 といえる。
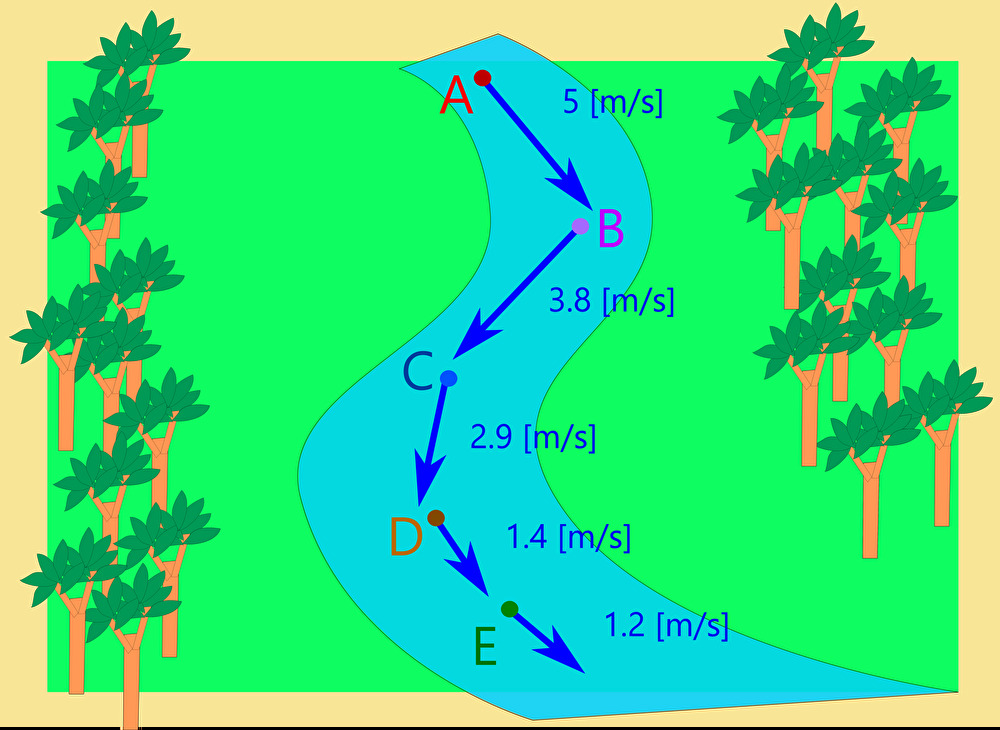
上の図のように川を水の速度という変数で着目したとき例えば 点A には大きさ 5.0 の 右下方向 の ベクトル が対応している。
このように空間内のある点に数字のみならず向きの情報も含まれているのが ベクトル場 の特徴である。
スカラー場は \(x\)、\(y\)、\(z\)を用いて \(f\left(x,y,z\right)\) と表されて、定数 \(c\) を用いて
$$f\left(x,y,z\right)=c$$
は 曲面 を意味する。この 曲面 を スカラー場 \(f\left(x,y,z\right)\) の 等位面 と呼ぶ。
ここで、大事なのは スカラー場 \(f\left(x,y,z\right)\) が 曲面 を直接的に表しているわけではないということである。スカラー場 はあくまで 分布 に過ぎず、分布 内の点のうち 定数 \(c\) となる点を線で繋ぐことで 曲面 を形成する。
スカラー場の例として、\(f\left(x,y,z\right)=x^{2}+y^{2}+z^{2}\) を考えてみよう。
このスカラー場をイラストで表現すると次のようになる。
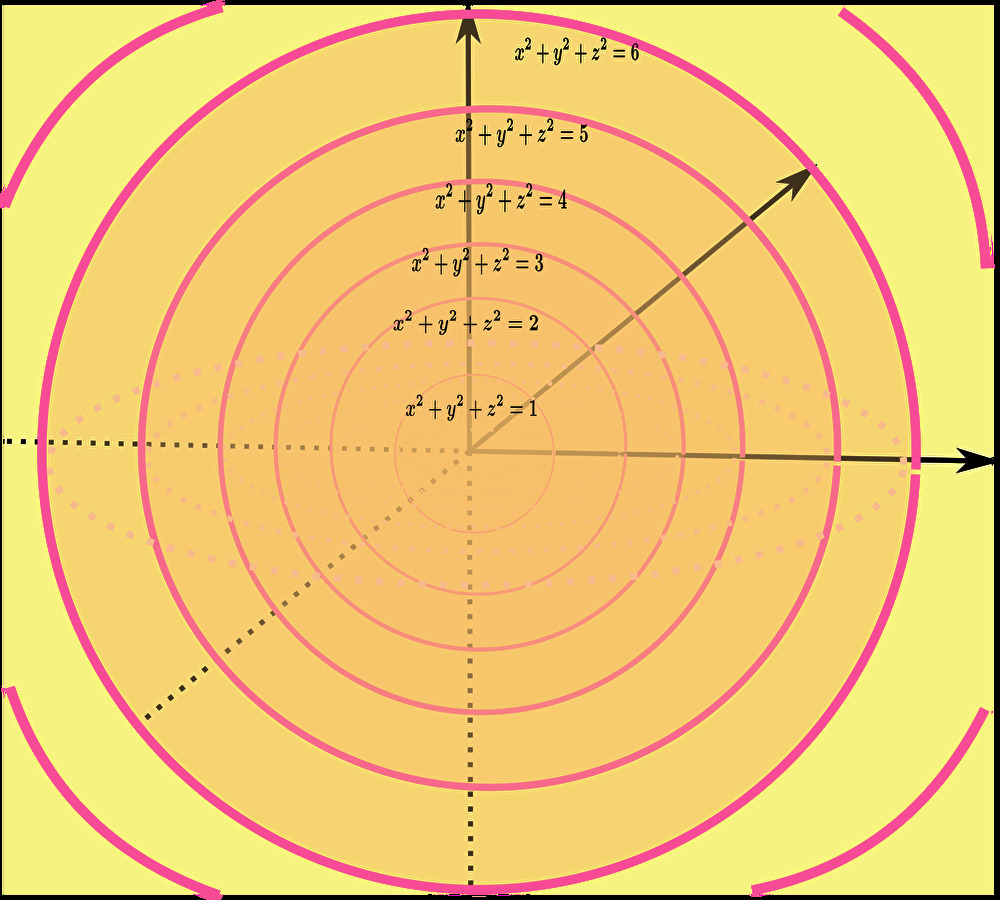
スカラー場 \(f\left(x,y,z\right)=x^{2}+y^{2}+z^{2}\) はこのように \(x^{2}+y^{2}+z^{2}=c\ \ \ \left(cは定数\right)\) の集合(分布)である。
ここで、例えば \(x^{2}+y^{2}+z^{2}=2\) が意味するものというのは上のスカラー場の図の \(x^{2}+y^{2}+z^{2}=2\) を切り取ったものとなる。

スカラー場の勾配 ~grad~
スカラー場 \(f\left(x,y,z\right)\) に対して、
$$\mathrm{grad}\ f=\displaystyle\frac{\partial f}{\partial x}\color{red}{\pmb{i}}+\displaystyle\frac{\partial f}{\partial y}\color{blue}{\pmb{j}}+\displaystyle\frac{\partial f}{\partial z}\color{green}{\pmb{k}}\cdot\cdot\cdot\left(A\right)$$
を \(f\left(x,y,z\right)\) の 勾配 と呼ぶ。勾配 は ベクトル場 であることに注意しよう。
曲線 の 微分 が曲線の 変化の勢い(接線の傾き)を表しているように、曲面 の 偏微分 は曲面の 変化の勢い を表している。
勾配 は スカラー場 \(f\left(x,y,z\right)\) の変化の勢いを表している。
例えば、スカラー場 \(f\left(x,y,z\right)=xyz\ \left(1\leq x,y,z\leq 5\right)\) の 勾配 を考えてみよう。
曲面 \(xyz=c\ \ \ \left(\ c\ は定数\right)\) の概形は次のアニメーションのように反り立つ壁のようになっている。

勾配となるベクトルは式 \(\left(A\right)\) のようにスカラー場の式を \(x\)、 \(y\)、 \(z\) でそれぞれ偏微分すれば各成分が求まるので
\begin{eqnarray}\mathrm{grad}\ f&=&\displaystyle\frac{\partial f}{\partial x}\color{red}{\pmb{i}}+\displaystyle\frac{\partial f}{\partial y}\color{blue}{\pmb{j}}+\displaystyle\frac{\partial f}{\partial z}\color{green}{\pmb{k}}\\\\&=&\displaystyle\frac{\partial}{\partial x}\left(xyz\right)\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial}{\partial y}\left(xyz\right)\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial}{\partial z}\left(xyz\right)\ \color{green}{\pmb{k}}\\\\&=&\left(yz\right)\ \color{red}{\pmb{i}}+\left(xz\right)\ \color{blue}{\pmb{j}}+\left(xy\right)\ \color{green}{\pmb{k}}\end{eqnarray}
と求まる。
この 勾配ベクトル は反り立つ壁(スカラー場)の変化の勢いを示している。
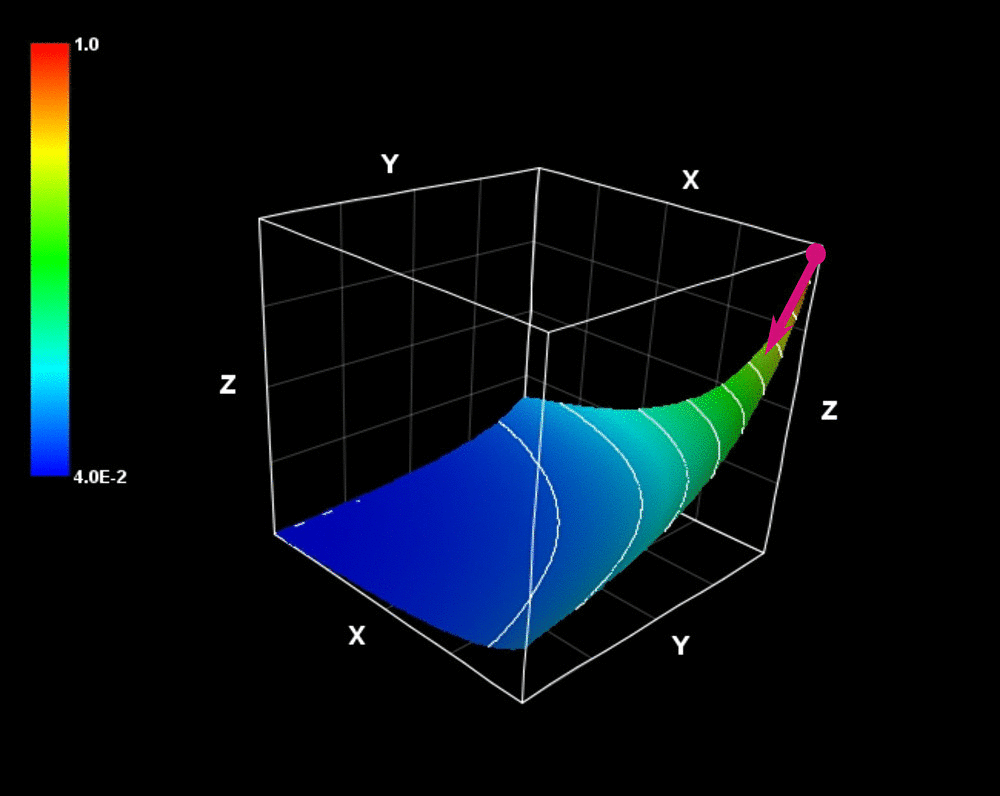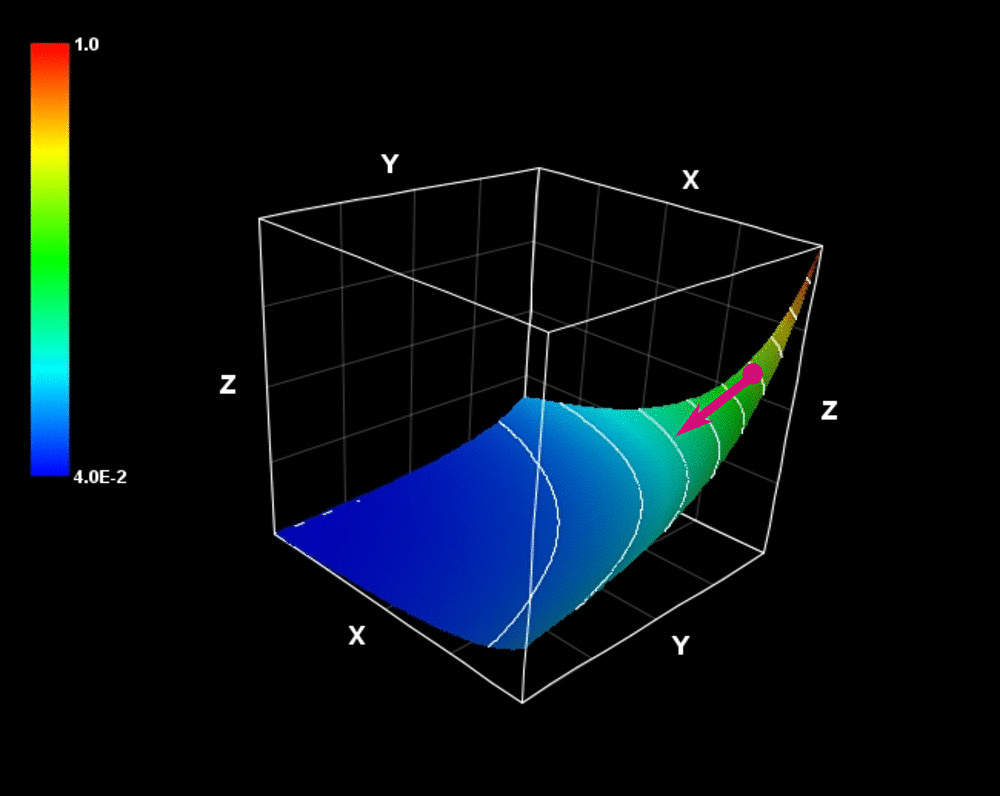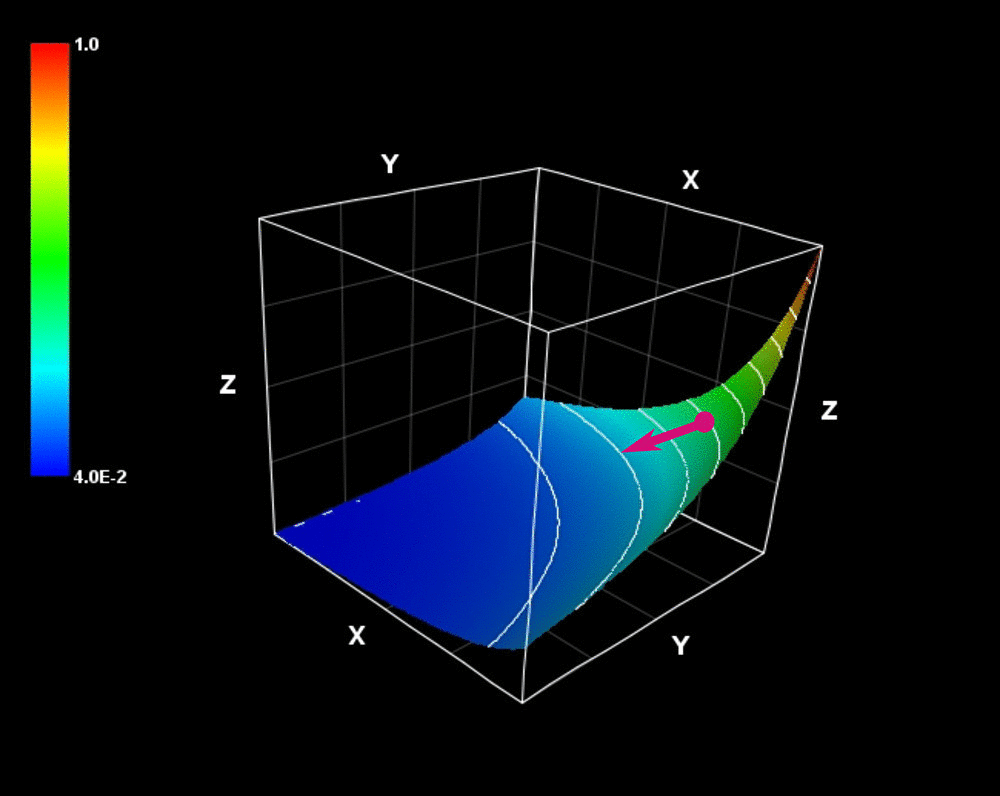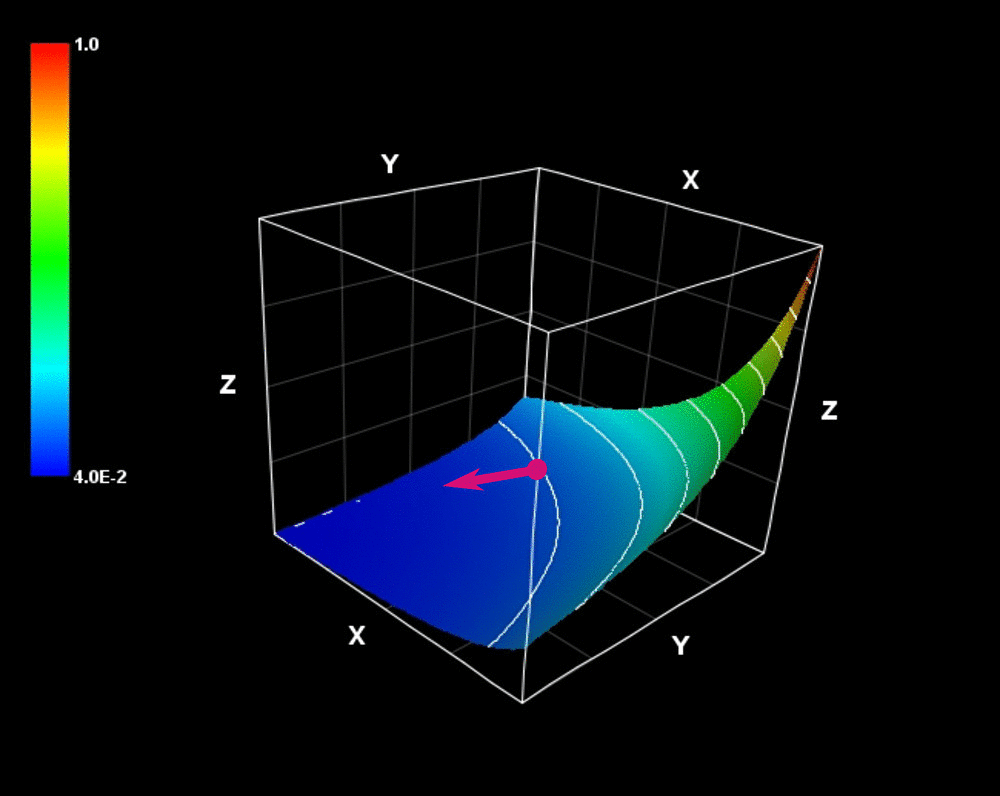
$$\mathrm{grad}\ f=\left(yz\right)\ \color{red}{\pmb{i}}+\left(xz\right)\ \color{blue}{\pmb{j}}+\left(xy\right)\ \color{green}{\pmb{k}}$$
例題
単位球面 \(x^{2}+y^{2}+z^{2}=1\) について点 \(\left(\displaystyle\frac{1}{2},\displaystyle\frac{1}{2},\displaystyle\frac{1}{\sqrt{2}}\right)\) における 勾配 を求めよ。
例題の解答
単位球面 \(x^{2}+y^{2}+z^{2}=1\) の スカラー場 は
$$f\left(x,y,z\right)=x^{2}+y^{2}+z^{2}$$
である。勾配となるベクトルは式 \(\left(A\right)\) のようにスカラー場の式を \(x\)、 \(y\)、 \(z\) でそれぞれ偏微分すれば各成分が求まるので
\begin{eqnarray}\mathrm{grad}\ f&=&\displaystyle\frac{\partial f}{\partial x}\color{red}{\pmb{i}}+\displaystyle\frac{\partial f}{\partial y}\color{blue}{\pmb{j}}+\displaystyle\frac{\partial f}{\partial z}\color{green}{\pmb{k}}\\\\&=&\displaystyle\frac{\partial}{\partial x}\left(x^{2}+y^{2}+z^{2}\right)\ \color{red}{\pmb{i}}+\displaystyle\frac{\partial}{\partial y}\left(x^{2}+y^{2}+z^{2}\right)\ \color{blue}{\pmb{j}}+\displaystyle\frac{\partial}{\partial z}\left(x^{2}+y^{2}+z^{2}\right)\ \color{green}{\pmb{k}}\\\\&=&\left(2x+0+0\right)\ \color{red}{\pmb{i}}+\left(0+2y+0\right)\ \color{blue}{\pmb{j}}+\left(0+0+2z\right)\ \color{green}{\pmb{k}}\\\\&=&\left(2x\right)\ \color{red}{\pmb{i}}+\left(2y\right)\ \color{blue}{\pmb{j}}+\left(2z\right)\ \color{green}{\pmb{k}}\end{eqnarray}
従って、単位球面 \(x^{2}+y^{2}+z^{2}=1\) の 勾配ベクトル は
$$\mathrm{grad}\ f=\left(2x\right)\ \color{red}{\pmb{i}}+\left(2y\right)\ \color{blue}{\pmb{j}}+\left(2z\right)\ \color{green}{\pmb{k}}$$
となる。
曲面(単位球面)上の 特定の点 \(\left(\displaystyle\frac{1}{2},\displaystyle\frac{1}{2},\displaystyle\frac{1}{\sqrt{2}}\right)\) における 勾配ベクトル は
勾配ベクトル \(\mathrm{grad}\ f=\left(2x\right)\ \color{red}{\pmb{i}}+\left(2y\right)\ \color{blue}{\pmb{j}}+\left(2z\right)\ \color{green}{\pmb{k}}\) に
\begin{cases}x&=&\displaystyle\frac{1}{2}\\\\ y&=&\displaystyle\frac{1}{2}\\\\ z&=&\displaystyle\frac{1}{\sqrt{2}}\end{cases}
を代入することで求まる。
\begin{eqnarray}\mathrm{grad}\ f&=&\left(2x\right)\ \color{red}{\pmb{i}}+\left(2y\right)\ \color{blue}{\pmb{j}}+\left(2z\right)\ \color{green}{\pmb{k}}\\\\&=&\left(2\cdot\displaystyle\frac{1}{2}\right)\ \color{red}{\pmb{i}}+\left(2\cdot\displaystyle\frac{1}{2}\right)\ \color{blue}{\pmb{j}}+\left(2\cdot\displaystyle\frac{1}{\sqrt{2}}\right)\ \color{green}{\pmb{k}}\\\\&=&\color{red}{\pmb{i}}+\color{blue}{\pmb{j}}+\sqrt{2}\ \color{green}{\pmb{k}}\end{eqnarray}
以上より単位球面上の点 \(\left(\displaystyle\frac{1}{2},\displaystyle\frac{1}{2},\displaystyle\frac{1}{\sqrt{2}}\right)\) における 勾配ベクトル は
$$\mathrm{grad}\ f=\color{red}{\pmb{i}}+\color{blue}{\pmb{j}}+\sqrt{2}\ \color{green}{\pmb{k}}$$
練習問題
スカラー場 \(f\left(x,y,z\right)=xy\sin{z}\) について 点 \(\left(1,1,\displaystyle\frac{\pi}{2}\right)\) における 勾配 を求めよ。
まとめ
・スカラー場 は 分布 を意味し、主に 等高線 で図示される。
・ベクトル場 は 流れ を意味し、主に ベクトルの集合 で図示される。
・勾配 は スカラー場 に対して定義されるもので、スカラー場 の変化の勢いを意味する。勾配 の式は
$$\mathrm{grad}\ f=\displaystyle\frac{\partial f}{\partial x}\color{red}{\pmb{i}}+\displaystyle\frac{\partial f}{\partial y}\color{blue}{\pmb{j}}+\displaystyle\frac{\partial f}{\partial z}\color{green}{\pmb{k}}$$
である。勾配 は ベクトル であることに注意!





