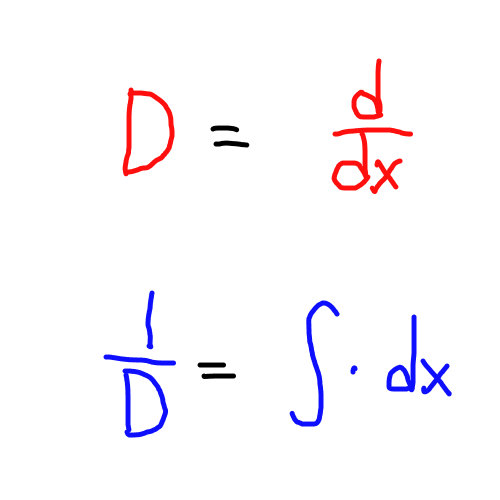2階線形微分方程式に対するファイナルウェポン
2階線形微分方程式$$y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)$$
の解法として
・右辺から解の形を予想する方法
・ロンスキアンを使う方法
を述べた。(それぞれ下記事参照)
今回は2階線形微分方程式に対する最後の手として「微分演算子」を用いた解法を説明する。


微分演算子
今回の記事の目玉である 微分演算子 \(D\) の紹介をする。
独立した変数 \(x\) による微分 \(\displaystyle\frac{d}{dx}\) を \(D\) と書くことにする。つまり、
$$\displaystyle\frac{dy}{dx}=Dy$$
$$\displaystyle\frac{d^{2}y}{dx^2}=\displaystyle\frac{d}{dx}\displaystyle\frac{dy}{dx}=D\cdot Dy=D^{2}y$$
と書ける。すなわち 微分演算子 \(D\) は「関数と左から掛け算することで微分する」力を持った記号を意味し、2回微分、3回微分はその2乗(\(D^2y\))、3乗(\(D^3y\)) で表現する。
例えば、2階線形微分方程式 \(y^{\prime\prime}-4y^{\prime}+3y=\mathrm{e}^{x}\) は微分演算子 \(D\) を用いることで
$$D^{2}y-4Dy+3y=\mathrm{e}^{x}$$
$$\left(D^{2}-4D+3\right)y=\mathrm{e}^{x}$$
と書けるようになる。
次に 微分演算子 \(D\) で割る、すなわち \(\displaystyle\frac{1}{D}\) で掛け算することとはどういうことなのか考えてみよう。
\(y’=Dy\) であるので、両辺を左から \(D\) で割ると
$$\displaystyle\frac{1}{D}y’=y$$
となる。\(\displaystyle\int y’dx=y\) と比較すると \(\displaystyle\frac{1}{D}\) が不定積分 \(\int\bigcirc dx\) を意味することが分かる。
今後2階線形微分方程式を 微分演算子 を用いて解くとき、次の公式を駆使して解いていく。
$$\displaystyle\frac{1}{\left(D-\alpha\right)^n}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^n}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot\left(A\right)$$
ただし \(n\) は指数を表す数
まず微分方程式
$$Dy-\alpha y=f\left(x\right)$$
$$\left(D-\alpha\right)y=f\left(x\right)$$
を考える。ここで突然だが指数関数と \(y\) の積の関数 \(\mathrm{e}^{-\alpha x}y\) を \(x\) で1回微分してみよう。すると
\begin{eqnarray}&&D\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D\mathrm{e}^{-\alpha x}\right)\cdot y+\mathrm{e}^{-\alpha x}\cdot\left(Dy\right)\\\\&=&\left(-\alpha\mathrm{e}^{-\alpha x}\right)\cdot y+\mathrm{e}^{-\alpha x}\cdot Dy\\\\&=&\mathrm{e}^{-\alpha x}\left(Dy-\alpha y\right)\\\\&=&\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\end{eqnarray}
ここで、 \(\left(D-\alpha\right)y=f\left(x\right)\) であるから
$$D\left(\mathrm{e}^{-\alpha x}y\right)= \mathrm{e}^{-\alpha x} f\left(x\right) $$
両辺を 微分演算子 \(D\) で左から割ると
$$\mathrm{e}^{-\alpha x}y=\displaystyle\frac{1}{D}\{\mathrm{e}^{-\alpha x} f\left(x\right) \}$$
両辺に \(\mathrm{e}^{\alpha x}\) をかけて
$$y= \mathrm{e}^{\alpha x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot \left(1\right) $$
元々 \(y\) は \(\left(D-\alpha\right)y=f\left(x\right)\) すなわち
$$y=\displaystyle\frac{1}{D-\alpha}f\left(x\right)\cdot\cdot\cdot \left(1’\right) $$
を満たすので式 \(\left(1\right)\)、\(\left(1’\right)\) から \(y\) を消去して
$$\displaystyle\frac{1}{D-\alpha}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}$$
となり、式(A)の \(n=1\) のときを導き出すことができた。
次に、微分方程式
$$\left(D-\alpha\right)^{2}y=f\left(x\right)$$
について考えてみよう。
先ほどと同様に指数関数と \(y\) の積の関数 \(\mathrm{e}^{-\alpha x}y\) を考える。 今回は \(x\) で2回微分してみよう。すると
$$D^{2}\left(\mathrm{e}^{-\alpha x}y\right)=D\left(D\mathrm{e}^{-\alpha x}y\right)$$
先ほど求めた \(D\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\) を代入すると
\begin{eqnarray}&&D^{2}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&D\left(D\mathrm{e}^{-\alpha x}y\right)\\\\&=&D\{\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\}\\\\&=&\left(D-\alpha \right)\cdot D\left(\mathrm{e}^{-\alpha x}y\right)\end{eqnarray}
\(D\left(\mathrm{e}^{-\alpha x}y\right)\) が出現したので、再度 \(D\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\) を代入すると
\begin{eqnarray}&&D^{2}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)\cdot D\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)\cdot\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\\\\&=&\mathrm{e}^{-\alpha x}\left(D-\alpha \right)^{2}y\end{eqnarray}
ここで、 \(\left(D-\alpha\right)^{2}y=f\left(x\right)\) であるから
$$D^{2}\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}f\left(x\right)$$
両辺を左から \(D^2\) で割ると
$$\mathrm{e}^{-\alpha x}y=\displaystyle\frac{1}{D^2}\{\mathrm{e}^{-\alpha x} f\left(x\right) \}$$
両辺に \(\mathrm{e}^{\alpha x}\) をかけて
$$y= \mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^2}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot \left(2\right) $$
元々 \(y\) は \(\left(D-\alpha\right)^{2}y=f\left(x\right)\) すなわち
$$y=\displaystyle\frac{1}{\left(D-\alpha\right)^{2}}f\left(x\right)\cdot\cdot\cdot \left(2’\right) $$
を満たすので式 \(\left(2\right)\)、\(\left(2’\right)\) から \(y\) を消去して
$$\displaystyle\frac{1}{\left(D-\alpha\right)^{2}}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^2}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}$$
となり、式(A)の \(n=2\) のときを導き出すことができた。
この調子で 一般の \(n\) について式(A)が成り立つことを示そう。
まずは微分方程式
$$\left(D-\alpha\right)^{n}y=f\left(x\right)$$
について考えてみよう。
\(n=1,2\) のときと同じように指数関数と \(y\) の積の関数 \(\mathrm{e}^{-\alpha x}y\) を考える。
この積を \(x\) で \(n\) 回微分してみよう。
すると \(D\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\) を用いて次のように計算できる。
\begin{eqnarray}&&D^{n}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&D^{n-1}\left(D\mathrm{e}^{-\alpha x}y\right)\\\\&=&D^{n-1}\{\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\}\\\\&=&\left(D-\alpha \right)\cdot D^{n-1}\left(\mathrm{e}^{-\alpha x}y\right)\end{eqnarray}
つまり \(D^{n}\left(\mathrm{e}^{-\alpha x}y\right)=\left(D-\alpha \right)\cdot D^{n-1}\left(\mathrm{e}^{-\alpha x}y\right)\)が成り立つ。これを \(n\) 回繰り返すと
\begin{eqnarray}&&D^{n}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)\cdot D^{n-1}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)\left(D-\alpha \right)\cdot D^{n-2}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)\left(D-\alpha \right)\left(D-\alpha \right)\cdot D^{n-3}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\cdot\cdot\cdot\\\\&=&\left(D-\alpha \right)^{n}\cdot D^{0}\left(\mathrm{e}^{-\alpha x}y\right)\end{eqnarray}
\(D^{0}\left(\mathrm{e}^{-\alpha x}y\right)\) について、\(D^{0}\) は「0回微分」つまり「微分しない」を意味するので、\(D^{0}\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}y\) となる。よって
\begin{eqnarray}&&D^{n}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)^{n}\cdot D^{0}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\left(D-\alpha \right)^{n}\mathrm{e}^{-\alpha x}y\end{eqnarray}
ここで、 \(\left(D-\alpha\right)^{n}y=f\left(x\right)\) であるから
$$D^{n}\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}f\left(x\right)$$
両辺を左から \(D^n\) で割ると
$$\mathrm{e}^{-\alpha x}y=\displaystyle\frac{1}{D^n}\{\mathrm{e}^{-\alpha x} f\left(x\right) \}$$
両辺に \(\mathrm{e}^{\alpha x}\) をかけて
$$y= \mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^n}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot \left(N\right) $$
元々 \(y\) は \(\left(D-\alpha\right)^{n}y=f\left(x\right)\) すなわち
$$y=\displaystyle\frac{1}{\left(D-\alpha\right)^{n}}f\left(x\right)\cdot\cdot\cdot \left(N’\right) $$
を満たすので式 \(\left(N\right)\)、\(\left(N’\right)\) から \(y\) を消去して
$$\displaystyle\frac{1}{\left(D-\alpha\right)^{n}}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^n}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}$$
となり式(A)を導き出すことができた。
場合によっては、公式(A)の亜種である下の公式(B)が必要となることも多い。
$$\displaystyle\frac{1}{\left(D-\alpha\right)^2+\beta^2}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^{2}+\beta^{2}}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot\left(B\right)$$
上の式(A)の導出を読んだ前提で話をする。
まず、微分方程式
$$\{\left(D-\alpha\right)^{2}+\beta^{2}\}y=f\left(x\right)$$
について考える。
またまた突然だが指数関数と \(y\) の積の関数 \(\mathrm{e}^{-\alpha x}y\) を考える。
この積に \(\left(D^{2}+\beta^{2}\right)\) をかけ算してみよう。
すると \(D\left(\mathrm{e}^{-\alpha x}y\right)=\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\) を用いて次のように計算できる。
\begin{eqnarray}&&\left(D^{2}+\beta^{2}\right)\mathrm{e}^{-\alpha x}y\\\\&=& D^{2}\left(\mathrm{e}^{-\alpha x}y\right)+\beta^{2}\mathrm{e}^{-\alpha x}y\\\\&=& D\left(D\mathrm{e}^{-\alpha x}y\right)+\beta^{2}\mathrm{e}^{-\alpha x}y\\\\&=& D\{\mathrm{e}^{-\alpha x}\left(D-\alpha \right)y\}+\beta^{2}\mathrm{e}^{-\alpha x}y\\\\&=&\left(D-\alpha \right)\cdot \left(D\mathrm{e}^{-\alpha x}y\right)+\beta^{2}\mathrm{e}^{-\alpha x}y\\\\&=&\left(D-\alpha \right)^{2}\mathrm{e}^{-\alpha x}y+\beta^{2}\left(\mathrm{e}^{-\alpha x}y\right)\\\\&=&\{\left(D-\alpha \right)^{2}+\beta^{2}\}\mathrm{e}^{-\alpha x}y\end{eqnarray}
ここで、 \( \{\left(D-\alpha\right)^{2}+\beta^{2}\}y= f\left(x\right) \) であるから
$$\left(D^{2}+\beta^{2}\right)\mathrm{e}^{-\alpha x}y=\mathrm{e}^{-\alpha x}f\left(x\right)$$
両辺を左から \(\left(D^{2}+\beta^{2}\right)\) で割ると
$$\mathrm{e}^{-\alpha x}y=\displaystyle\frac{1}{D^{2}+\beta^{2}}\{\mathrm{e}^{-\alpha x} f\left(x\right) \}$$
両辺に \(\mathrm{e}^{\alpha x}\) をかけて
$$y= \mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^{2}+\beta^{2}}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}\cdot\cdot\cdot \left(I\right) $$
元々 \(y\) は \(\{\left(D-\alpha\right)^{2}+\beta^{2}\}y=f\left(x\right)\) すなわち
$$y=\displaystyle\frac{1}{\left(D-\alpha\right)^{2}+\beta^{2}}f\left(x\right)\cdot\cdot\cdot \left(I’\right) $$
を満たすので式 \left(I\right)、\left(I^{\prime}\right)から \(y\) を消去して
$$\displaystyle\frac{1}{\left(D-\alpha\right)^{2}+\beta^{2}}f\left(x\right)=\mathrm{e}^{\alpha x}\displaystyle\frac{1}{D^{2}+\beta^{2}}\{\mathrm{e}^{-\alpha x}f\left(x\right)\}$$
となり式(B)を導き出すことができた。
式(B)の右辺をさらに簡単化できる次の公式(C)も紹介する。
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{\sin{\beta x}}{\beta}\displaystyle\frac{1}{D}\{f\left(x\right)\cos{\beta x}\}-\displaystyle\frac{\cos{\beta x}}{\beta}\displaystyle\frac{1}{D}\{f\left(x\right)\sin{\beta x}\}\cdot\cdot\cdot\left(C\right)$$
\(\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)\) について部分分数分解を施すと
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{1}{2\beta\mathit{i}}\left[\displaystyle\frac{1}{D-\beta\mathit{i}}f\left(x\right)-\displaystyle\frac{1}{D+\beta\mathit{i}}f\left(x\right)\right]$$
上の公式(A)より
$$\displaystyle\frac{1}{D\pm\beta\mathit{i}}f\left(x\right)=\mathrm{e}^{\mp\beta\mathit{i} x}\displaystyle\frac{1}{D}\{\mathrm{e}^{\pm\beta\mathit{i} x}f\left(x\right)\}$$
であるので
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{1}{2\beta\mathit{i}}\left[\mathrm{e}^{\mathit{i}\beta x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-\mathit{i}\beta x}f\left(x\right)\}-\mathrm{e}^{-\mathit{i}\beta x}\displaystyle\frac{1}{D}\{\mathrm{e}^{\mathit{i} \beta x}f\left(x\right)\}\right]$$
さて、オイラーの公式 \(\mathrm{e}^{\mathit{i}\theta}=\cos{\theta}+\mathit{i}\sin{\theta}\) を代入すると
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{1}{2\beta\mathit{i}}\left[\left(\cos{\beta x}+\mathit{i}\sin{\beta x}\right)\displaystyle\frac{1}{D}\{\left(\cos{\left(-\beta x\right)}+\mathit{i}\sin{\left(-\beta x\right)}\right)f\left(x\right)\}-\left(\cos{\left(-\beta x\right)}+\mathit{i}\sin{\left(-\beta x\right)}\right)\displaystyle\frac{1}{D}\{\left(\cos{\beta x}+\mathit{i}\sin{\beta x}\right)f\left(x\right)\}\right]$$
偶関数、奇関数の性質から
\(\cos{-\theta}=\cos{\theta}\)、
\(\sin{-\theta}=-\sin{\theta}\)
であるので
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{1}{2\beta\mathit{i}}\left[\left(\cos{\beta x}+\mathit{i}\sin{\beta x}\right)\displaystyle\frac{1}{D}\{\left(\cos{\beta x}-\mathit{i}\sin{\beta x}\right)f\left(x\right)\}-\left(\cos{\beta x}-\mathit{i}\sin{\beta x}\right)\displaystyle\frac{1}{D}\{\left(\cos{\beta x}+\mathit{i}\sin{\beta x}\right)f\left(x\right)\}\right]$$
\(\displaystyle\frac{1}{D}\) は不定積分であるので、
$$\displaystyle\int\{f\left(x\right)+g\left(x\right)\}dx=\displaystyle\int\{f\left(x\right)\}dx+\displaystyle\int\{g\left(x\right)\}dx$$
を意識すると
\(\displaystyle\frac{1}{D}\{f\left(x\right)+g\left(x\right)\}=\displaystyle\frac{1}{D}\{f\left(x\right)\}+\displaystyle\frac{1}{D}\{g\left(x\right)\}\)
が成り立つ。
従って、
\begin{eqnarray}\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=&&\displaystyle\frac{1}{2\beta\mathit{i}}\left(\cos{\beta x}+\mathit{i}\sin{\beta x}\right)\left[\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\}\right]\\\\&&-\displaystyle\frac{1}{2\beta\mathit{i}}\left(\cos{\beta x}-\mathit{i}\sin{\beta x}\right)\left[\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}+\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\}\right]\end{eqnarray}
つまり
\begin{eqnarray} \displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)= \displaystyle\frac{1}{2\beta\mathit{i}}\left[\cos{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}+\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\cos{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\}-\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\}\\\\ -\cos{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}+\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\cos{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)+\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\}\}\right] \end{eqnarray}
右辺を計算して
\begin{eqnarray} \displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)&=&\displaystyle\frac{1}{2\beta\mathit{i}}\left[\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\cos{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)+\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\cos{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\right]\\\\&=&\displaystyle\frac{1}{2\beta\mathit{i}}\left[2\mathit{i}\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-2\cos{\beta x}\displaystyle\frac{1}{D}\{\mathit{i}\sin{\beta x}f\left(x\right)\right]\end{eqnarray}
すなわち
\begin{eqnarray} &&\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)\\\\&=&\displaystyle\frac{1}{\beta}\left[\sin{\beta x}\displaystyle\frac{1}{D}\{\cos{\beta x}f\left(x\right)\}-\cos{\beta x}\displaystyle\frac{1}{D}\{\sin{\beta x}f\left(x\right)\right]\end{eqnarray}
$$\displaystyle\frac{1}{D^{2}+\beta^{2}}f\left(x\right)=\displaystyle\frac{\sin{\beta x}}{\beta}\displaystyle\frac{1}{D}\{f\left(x\right)\cos{\beta x}\}-\displaystyle\frac{\cos{\beta x}}{\beta}\displaystyle\frac{1}{D}\{f\left(x\right)\sin{\beta x}\}$$
となり式(C)を求めることができた。
例題
例題1
\(y^{\prime\prime}-2y^{\prime}+y=0\) を解け。
例題2
\(y^{\prime\prime}+2y^{\prime}+2y=0\) を解け。
例題3
\(y^{\prime\prime}-3y^{\prime}+2y=\mathrm{e}^{x}\) を解け。
例題の解答
例題1
微分演算子を用いて微分方程式を書き直すと
$$D^{2}y-2Dy+y=0$$
$$\left(D^2-2D+1\right)y=0$$
$$\left(D-1\right)^{2}y=0$$
両辺を左から \(\left(D-1\right)^{2}\) で割ると
$$y=\displaystyle\frac{1}{\left(D-1\right)^{2}}\cdot \{0\}$$
ここで公式(A)より、
$$\displaystyle\frac{1}{\left(D-1\right)^{2}}\cdot \{0\}=\mathrm{e}^{x}\displaystyle\frac{1}{D^2}\{\mathrm{e}^{-x}\cdot 0\}$$
であるから
\begin{eqnarray}y&=&\mathrm{e}^{x}\displaystyle\frac{1}{D^2}\{\mathrm{e}^{-x}\cdot 0\}\\\\&=&\mathrm{e}^{x}\displaystyle\frac{1}{D^2}\cdot \{0\}\end{eqnarray}
ここで \(\displaystyle\frac{1}{D^2}\) は \(x\) での2回積分を表すので
\begin{eqnarray}y&=&\mathrm{e}^{x}\displaystyle\frac{1}{D^2}\cdot \{0\}\\\\&=&\mathrm{e}^{x}\int\int\{0\}dxdx\\\\&=&\mathrm{e}^{x}\int\left(C_{1}\right)dx\\\\&=&\mathrm{e}^{x}\left(C_{2}+xC_{1}\right)\end{eqnarray}
従って、求める微分方程式の解は
$$y= \mathrm{e}^{x}\left(C_{2}+xC_{1}\right) $$
例題2
微分演算子を用いて微分方程式を書き直すと
$$D^{2}y+2Dy+2y=0$$
$$\left(D^{2}+2D+2\right)y=0$$
左辺について平方完成すると
$$\{\left(D+1\right)^{2}+1\}y=0$$
つまり
$$y=\displaystyle\frac{1}{\left(D+1\right)^{2}+1}\cdot \{0\}$$
公式(B)より
$$y=\mathrm{e}^{- x}\displaystyle\frac{1}{D^{2}+1}\{\mathrm{e}^{x}\cdot{0}\}$$
さらに公式(C)を用いて
$$y=\sin{x}\displaystyle\frac{1}{D}\{0\cdot\cos{x}\}-\cos{x}\displaystyle\frac{1}{D}\{0\cdot\sin{x}\}$$
$$y=\sin{x}\displaystyle\frac{1}{D}\{0\}-\cos{x}\displaystyle\frac{1}{D}\{0\}$$
ここで、\(\displaystyle\frac{1}{D}\{\bigcirc\}\) は \(x\) による1階積分を表すので
$$y=\sin{x}\int\{0\}dx-\cos{x}\int\{0\}dx$$
従って定数 \(c_1\)、\(c_{2}\) を用いて
$$y=c_{1}\sin{x}-c_{2}\cos{x}$$
と書ける。\(C_{1}=c_{1}\)、\(C_{2}=-c_{2}\) と置けば
$$y=C_{1}\sin{x}+C_{2}\cos{x}$$
例題3
微分演算子を用いて微分方程式を書き直すと
$$D^2y-3Dy+2y=\mathrm{e}^{x}$$
$$\left(D^{2}-3D+2\right)y=\mathrm{e}^{x}$$
$$\left(D-1\right)\left(D-2\right)y=\mathrm{e}^{x}$$
両辺を \(\left(D-1\right)\left(D-2\right)\) で割ると
$$y=\displaystyle\frac{1}{\left(D-1\right)\left(D-2\right)}\mathrm{e}^{x}$$
右辺について部分分数分解を施して
\begin{eqnarray}y&=&\left(\displaystyle\frac{1}{D-2}-\displaystyle\frac{1}{D-1}\right)\mathrm{e}^{x}\\\\&=&\displaystyle\frac{1}{D-2}\{\mathrm{e}^{x}\}-\displaystyle\frac{1}{D-1}\{\mathrm{e}^{x}\}\end{eqnarray}
ここで公式(A)より、
\begin{eqnarray}\displaystyle\frac{1}{\left(D-2\right)}\cdot \{\mathrm{e}^{x}\}&=&\mathrm{e}^{2x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-2x}\cdot \mathrm{e}^{x}\}\\\\&=&\mathrm{e}^{2x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-x}\}\end{eqnarray}
\begin{eqnarray}\displaystyle\frac{1}{\left(D-1\right)}\cdot \{\mathrm{e}^{x}\}&=&\mathrm{e}^{x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-x}\cdot \mathrm{e}^{x}\}\\\\&=&\mathrm{e}^{x}\displaystyle\frac{1}{D}\{1\}\end{eqnarray}
と変形できるので
$$y=\mathrm{e}^{2x}\displaystyle\frac{1}{D}\{\mathrm{e}^{-x}\}-\mathrm{e}^{x}\displaystyle\frac{1}{D}\{1\}$$
ここで、\(\displaystyle\frac{1}{D}\{\bigcirc\}\) は \(x\) による1階積分を表すので
$$y=\mathrm{e}^{2x}\int\{\mathrm{e}^{-x}\}dx-\mathrm{e}^{x}\int\{1\}dx$$
$$y=\mathrm{e}^{2x}\left(-\mathrm{e}^{-x}+C_1\right)-\mathrm{e}^{x}\left(x+C_2\right)$$
$$y=\mathrm{e}^{2x}\left(-\mathrm{e}^{-x}+C_1\right)-\mathrm{e}^{x}\left(x+C_2\right)$$
練習問題
練習問題1
\(y^{\prime\prime}-6y^{\prime}+8y=0\) を解け。
練習問題2
\(y^{\prime\prime}+4y^{\prime}+4y=0\) を解け。
練習問題3
\(y^{\prime\prime}+2y^{\prime}+5y=0\) を解け。
練習問題4
\(y^{\prime\prime}-5y^{\prime}+6y=x\) を解け。
練習問題5
\(y^{\prime\prime}-6y^{\prime}+9y=\mathrm{e}^{3x}\cos{x}\) を解け。
ひとこと
2階線形微分方程式において、特性方程式が
・異なる二つの実数解を持つパターン
・重解を持つパターン
においては公式(A)のみで賄えるが、一方で
・複素数解を持つパターン
に対しては公式(B)、(C)のコンボをお見舞いしてあげなければならない。
また、2階線形微分方程式の解き方として
「解予想」「ロンスキアン」「微分演算子」の3つの方法を紹介したが
予想後の未定係数を求める連立方程式を解くのが困難だが直感的に解ける「解予想」
行列式の計算や符号管理で手間がかかるが万能な「ロンスキアン」
部分分数分解や3つの公式を使いこなす必要があるが万能な「微分演算子」
といったように、特別この方法が楽ちんだというものはない。(若干微分演算子は万能さで他2つより有利)
気に入った方法、しっくりくる方法を使っていこう。