例題を解きながら行列の階数(ランク、rank)の具体的な求め方を複数の視点から解説します。行列の階数は行列の特性を調べるために重要な考え方です。
行列の階数とは?
行列の階数とは、その行列の簡約化の主成分の個数のことである。
すなわち、階数を求めるには行列を簡約化すればよい!
例題
次の行列 \(A\) の階数(\(\mathrm{rank}\:A\))を求めよ。
$$A=\begin{pmatrix}0 & -3 & 3 & -2 & 1 & -7 \\0 & -3 & 3 & -2 & 1 & -7 \\0 & 3 & -3 & 2 & 0 & 9\\0 & -2 & 2 & -1 & 1 & -4 \end{pmatrix}$$
No.1:行列を簡約化する
$$\begin{pmatrix}0 & -3 & 3 & -2 & 1 & -7 \\0 & -3 & 3 & -2 & 1 & -7\\0 & 3 & -3 & 2 & 0 & 9 \\0 & -2 & 2 & -1 & 1 & -4 \end{pmatrix}$$
$$\rightarrow\begin{pmatrix}0 & 1 & -1 & 0 & 0 & 3 \\0 & 0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 0 & 1 & 2 \\0 & 0 & 0 & 0 & 0 & 0\end{pmatrix}$$

No.2:簡約化した行列の主成分の個数を数える
主成分の数が3個なので、階数(\(\mathrm{rank}\:A\))は3になる。
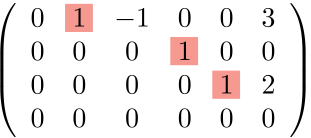
階数が3であることは、簡約化した行列の他の見方でも求められる。
階段の段数→3段
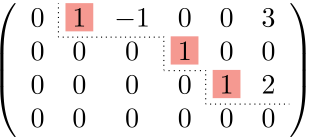
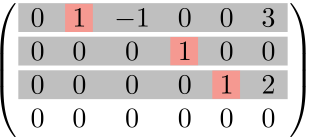
零ベクトルでない行の個数→3個
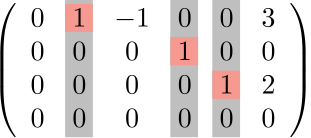
主成分を含む列の個数→3個
$$\mathrm{rank}\:A=3$$
まとめ
- 行列の階数は、その行列を簡約化することでわかる!
- 行列の階数は、簡約化の主成分の個数を数える!
同値表現
行列の階数には同値表現がある。
最も重要なのは、階数と一次独立の関係性を示す同値表現である。
「\(\mathrm{rank}\:A=A\) の列ベクトルの一次独立なものの最大個数」
そのため、階数によってベクトルの一次独立の判定などができる。





