例題を解きながら逆行列を簡約化を用いて求める方法をコツを交えながらわかりやすく解説します。逆行列は行列の逆数に相当する概念であり、定義とその求め方の両方を理解しておくことが大切です。
逆行列とは?
正方行列 \(A\) に対し、積が単位行列 \(E\) となる行列を \(A\) の逆行列といい、\(A^{-1}\)と表す。
逆行列の例
\(A=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\)、\(A^{-1}=\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}\) のとき、
$$\begin{eqnarray}AA^{-1}&=&\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}\\&=&\begin{pmatrix}1 & 0 & 0 \\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}=E\end{eqnarray}$$
逆行列は数字の逆数に相当する考え方である。
$$AA^{-1}=A^{-1}A=E$$
$$a\cdot a^{-1}=a^{-1}\cdot a=1$$
逆行列の求め方
行列 \(A\) が分かっている場合、逆行列 \(A^{-1}\) は、行列 \(A\) と単位行列 \(E\) を横に書き並べた行列を簡約化し、右半分を取り出すことで求められる。
逆行列の求め方
$$[A| E]\rightarrow[E| A^{-1}]$$
正方行列 \(A\) と標準基底 \(\{\vec e_1,\cdots,\vec e_n\}\) による複数の連立一次方程式
$$\begin{eqnarray}A\vec x&=&\vec e_1\\&\vdots&\\A\vec x&=&\vec e_n\end{eqnarray}$$
のそれぞれの唯一解を \(\{\vec x_1,\cdots,\vec x_n\}\) とおくと、
$$\begin{eqnarray}A\vec x_1&=&\vec e_1\\&\vdots&\\A\vec x_n&=&\vec e_n\end{eqnarray}$$
が成り立つ。よって、
$$\begin{eqnarray}A\begin{pmatrix}\vec x_1&\cdots&\vec x_n\end{pmatrix}&=&\begin{pmatrix}A\vec x_1&\cdots&A\vec x_n\end{pmatrix}\\&=&\begin{pmatrix}\vec e_1&\cdots&\vec e_n\end{pmatrix}\\&=&E\end{eqnarray}$$
となるため、\(A^{-1}=\begin{pmatrix}\vec x_1&\cdots&\vec x_n\end{pmatrix}\) とおけば、\(AA^{-1}=E\) が成り立つ。
つまり、複数の連立一次方程式の解 \(\{\vec x_1,\cdots,\vec x_n\}\) を求めればよいのだが、1つずつ簡約化して解くのは面倒である。
実際にそれぞれの拡大係数行列の簡約化を考えると、
$$\begin{eqnarray}[A| e_1]&\rightarrow&[E| x_1]\\&\vdots&\\ [A| e_n]&\rightarrow&[E| x_n]\end{eqnarray}$$
となる。これらの簡約化の手順は \(\{\vec e_1,\cdots,\vec e_n\}\) に依存しないため同時に行うことができ、
$$[A|\begin{matrix}\vec e_1&\cdots&\vec e_n\end{matrix}]\rightarrow[E| \begin{matrix}\vec x_1&\cdots&\vec x_n\end{matrix}]$$
すなわち、
$$[A| E]\rightarrow[E| A^{-1}]$$
となる。つまり、行列 \(A\) と単位行列 \(E\) を横に書き並べた行列 \([A| E]\) を簡約化すれば、右半分に逆行列 \(A^{-1}\) が求まるのである。
例題
次の行列の逆行列を求めよ。
$$A=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}$$
No.1:行列と単位行列を横に書き並べて新しい行列を作る
$$[A|E]=\left(\begin{array}{ccc|ccc}2 & -2 & -1& 1 & 0 & 0\\1 & -2 & -2 & 0 & 1 & 0\\-1 & 3 & 4 & 0 & 0 & 1\end{array}\right)$$
No.2:作った行列を簡約化する
$$\left(\begin{array}{ccc|ccc}2 & -2 & -1& 1 & 0 & 0\\1 & -2 & -2 & 0 & 1 & 0\\-1 & 3 & 4 & 0 & 0 & 1\end{array}\right)$$
$$\rightarrow\left(\begin{array}{ccc|ccc}1 & 0 & 0& 2 & -5 & -2 \\0 & 1 & 0 & 2 & -7 & -3\\0 & 0 & 1 & -1 & 4 & 2\end{array}\right)$$

行列が逆行列をもつ場合、簡約化すると単位行列 \(E\) になる!
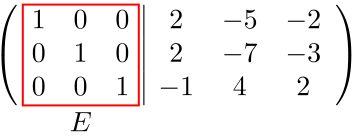
注:単位行列 \(E\) にならない場合は、逆行列をもたない
No.3:簡約化した行列の右半分を取り出す
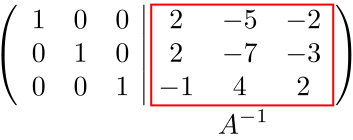
$$A^{-1}=\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}$$
検算
行列 \(A\) に逆行列 \(A^{-1}\) を掛けて単位行列になるか確認する。
$$AA^{-1}=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}=\begin{pmatrix}1 & 0 & 0 \\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}$$
まとめ
- 逆行列とは、正方行列に対して積が単位行列となる行列のことである!
- 逆行列は、行列と単位行列を横に書き並べて簡約化すれば求まる!