アニメーションを用いて余因子行列を利用して逆行列を求める方法を視覚的にわかりやすく解説します。また、計算ミスを防ぐためのコツも合わせて紹介します。
余因子行列とは?
余因子行列とは、正方行列 \(A\) に対して各成分が以下の法則で求められる正方行列のことであり、\(\tilde A\) と表される。
正方行列 \(A\) に対し、余因子行列 \(\tilde A\) の \((\color{red}{i},\color{blue}{j})\) 成分は、
\(A\) の第 \(\color{blue}{j}\) 行と第 \(\color{red}{i}\) 列を除いた行列の行列式に、符号 \((-1)^{\color{blue}{j}+\color{red}{i}}\) を掛けたもの。
注:第 \(\color{red}{i}\) 行と第 \(\color{blue}{j}\) 列を除くわけではない!
(例)3次の余因子行列
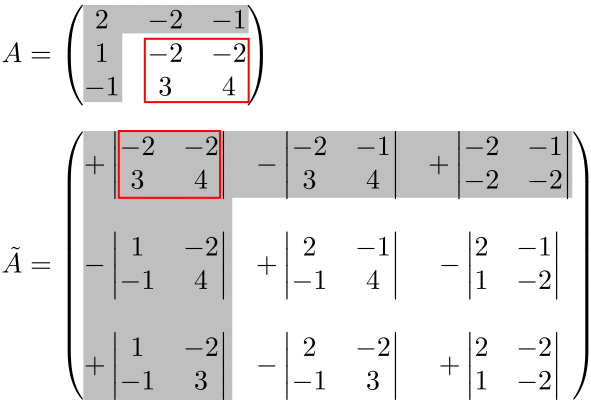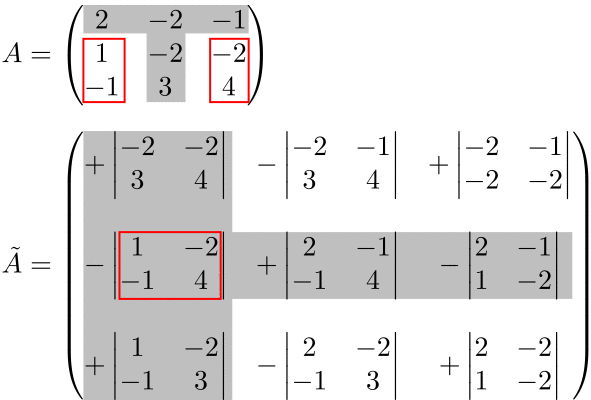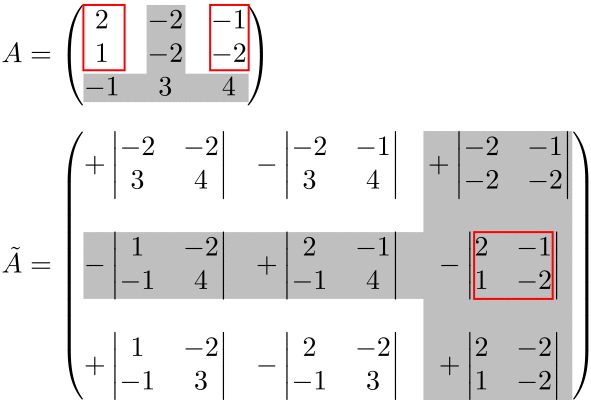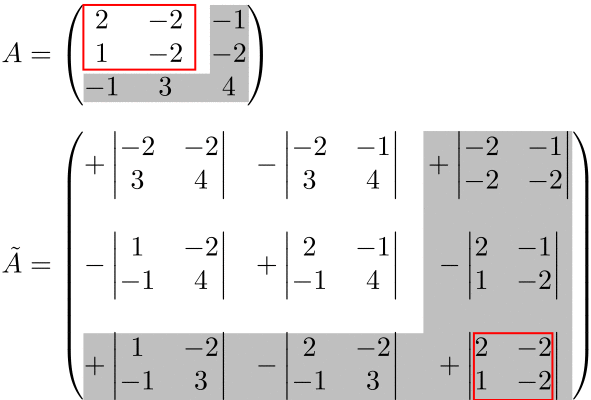
余因子行列の符号は、 \((-1)^{j+i}\) を表にした「符号表」を書くと分かりやすい。
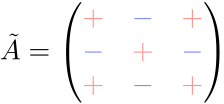
余因子行列と逆行列の関係
正方行列 \(A\) の逆行列 \(A^{-1}\) とは、\(AA^{-1}=E\)(単位行列)を満たす行列である。
余因子行列を用いると、次の定理から逆行列を求めることができる。
正方行列 \(A\) が逆行列をもつ必要十分条件はその行列式 \(|A|\neq 0\) であり、このとき逆行列 \(A^{-1}\) は余因子行列 \(\tilde A\) を用いて以下の方法で求められる。
$$A^{-1}=\frac{\tilde A}{|A|}$$
余因子行列を用いるメリット
逆行列を求めるには、行列を簡約化する方法もあった。

一方、簡約化よりも余因子行列を用いて逆行列を求める方が有効な場合がある。
- 行列のサイズが小さい場合(2次および3次)
- 行列に分数や文字が含まれる場合
- 逆行列が関係する証明問題を解く場合
そのため、簡約化による方法と使い分けをする必要がある。
2次または3次の行列に文字が含まれる場合は余因子行列を使おう!
余因子行列の計算ミスを減らすテクニック
余因子行列は成分の行・列と、行列式で除く行・列が反転しているため、非常に計算ミスを招きやすい。
反転の分かりにくさを解消するテクニックが、先に余因子行列の転置行列 \(\tilde A^{\top}\) を求める方法である。
転置余因子行列は、成分の行・列と、行列式で除く行・列が一致する。
(例)3次の転置余因子行列
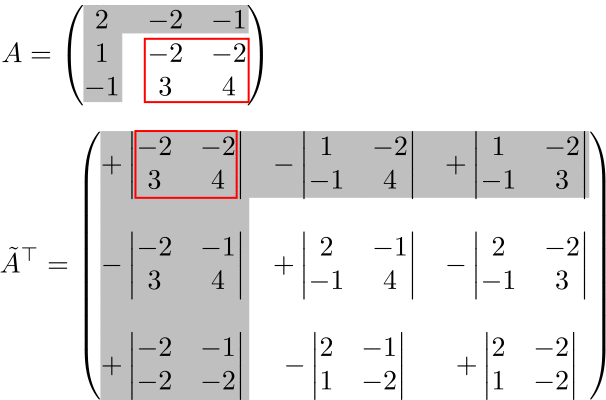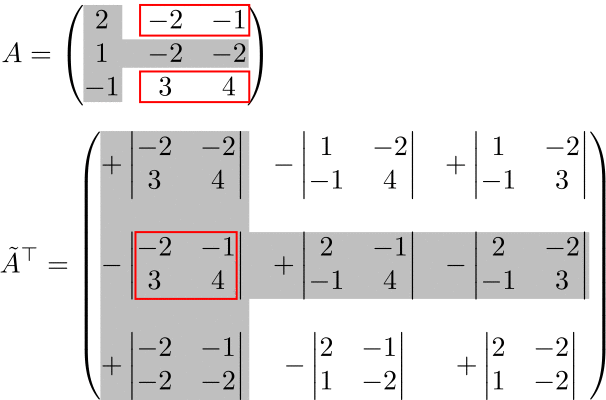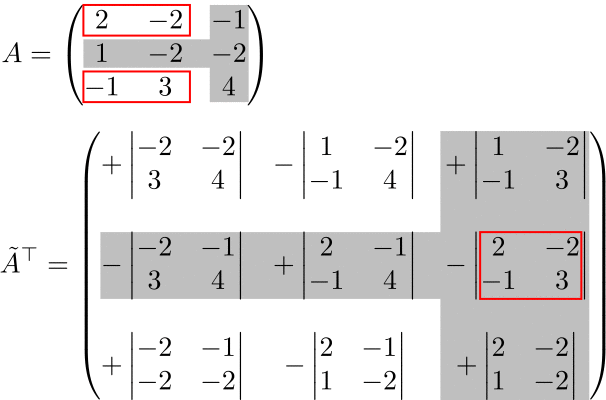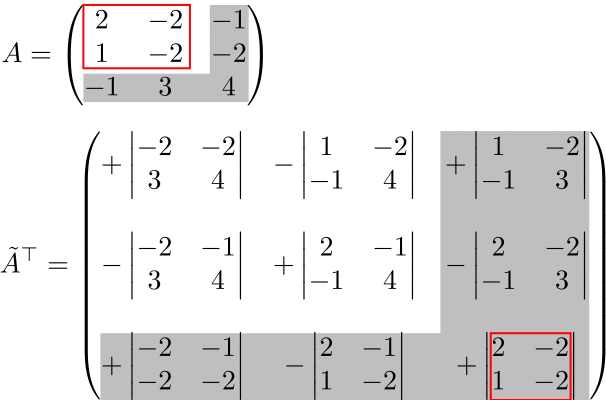
転置余因子行列の符号表は元の符号表と変わらない。
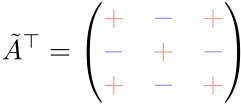
\(\tilde A^{\top}\) を求めた後、その行列を転置すれば \(\tilde A\) を求められる。
例題
次の行列の逆行列を求めよ。
$$A=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}$$
No.1:転置余因子行列の符号を書き込む
符号表に則って書き込めば簡単である。
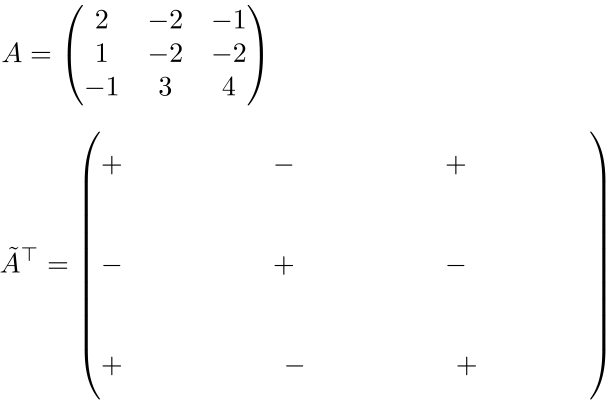
No.2:転置余因子行列の求めたい成分を1つ選ぶ
ここでは、例として \((1,1)\) 成分を選ぶ。
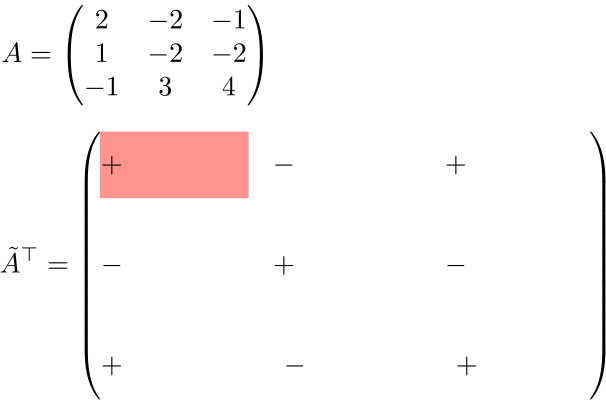
No.3:選んだ成分の行・列を除いた行列式を書き込む
\((1,1)\) 成分を選んでいることから、行列 \(A\) の第1行と第1列を除いた行列の行列式を書き込む。

No.4:No.2〜No.3を繰り返す

No.5:成分を計算して転置する
$$\tilde A^{\top}=\begin{pmatrix}-2 & -2 & 1 \\5 & 7 & -4\\2 & 3 & -2\end{pmatrix}$$
$$\tilde A=(\tilde A^{\top})^{\top}=\begin{pmatrix}-2 & 5 & 2 \\-2 & 7 & 3\\1 & -4 & -2\end{pmatrix}$$
No.6:定理を用いて逆行列を計算する
\(|A|=-1\) より、
$$A^{-1}=\frac{\tilde A}{|A|}=-\begin{pmatrix}-2 & 5 & 2 \\-2 & 7 & 3\\1 & -4 & -2\end{pmatrix}=\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}$$

$$A^{-1}=\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}$$
検算
行列 \(A\) に逆行列 \(A^{-1}\) を掛けて単位行列になるか確認する。
$$AA^{-1}=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\begin{pmatrix}2 & -5 & -2 \\2 & -7 & -3\\-1 & 4 & 2\end{pmatrix}=\begin{pmatrix}1 & 0 & 0 \\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}$$
まとめ
- 余因子行列とは、正方行列に対して各成分が行・列を反転した余因子である行列である!
- 余因子行列を用いると、逆行列を求めることができる!