アニメーションを用いてクラーメルの公式で連立一次方程式を解く様子を例題を交えながら視覚的にわかりやすく解説します。
クラーメルの公式とは?
クラーメルの公式とは、連立一次方程式の解を行列式を用いて一発で求める方法のことである。
計算方法は以下に示す通りである。
- 求めたい変数を選ぶ
- ①で選んだ変数に対応する係数行列の列を、列ベクトルに置き換えて行列式を計算
- ②を係数行列の行列式で割る
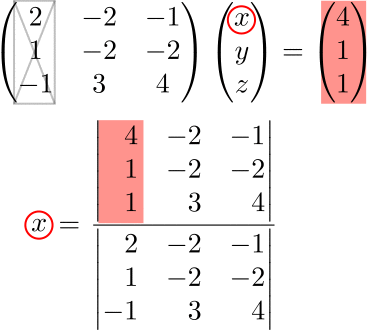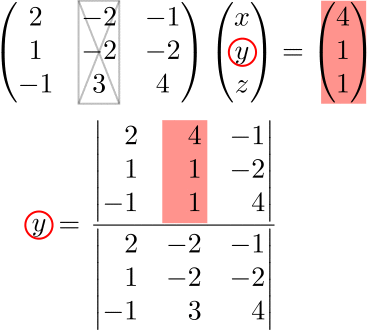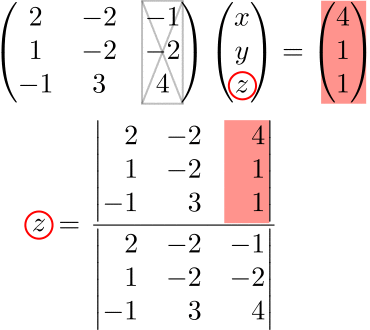
クラーメルの公式のメリット
連立一次方程式の解を求める方法には、掃き出し法があった。
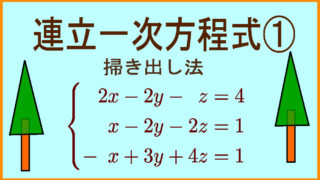
一方、掃き出し法よりもクラーメルの公式を用いる方法が有効な場合がある。
- 連立一次方程式の変数が少ないとき(2つのときが特に有効)
- 変数の1つだけを求めればよい場合( \(x\) だけ求める場合など)
- 係数行列に分数や文字が含まれている場合
- 連立一次方程式の解の成分を用いる証明問題を解く場合
変数を1つだけピンポイントで求める問題ではクラーメルの公式を使おう!
クラーメルの公式の注意点
クラーメルの公式では、分母に係数行列 \(A\) の行列式 \(|A|\) が来るため、\(|A|\neq0\) でなければならないことに注意しよう。( \(|A|=0\) の場合は解が1つに決まらない)
また、行列式の計算は次数が高くなるほど計算量が増えるため、クラーメルの公式は2次か3次で使うのを推奨する。
2次および3次の行列式はサラスの方法を使用しよう!
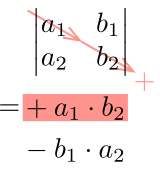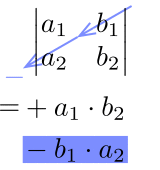
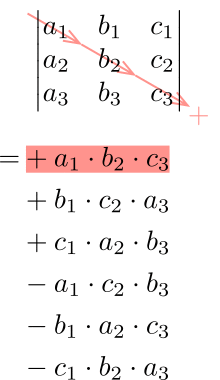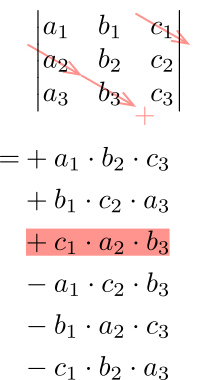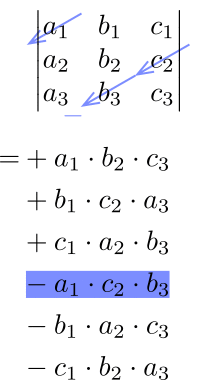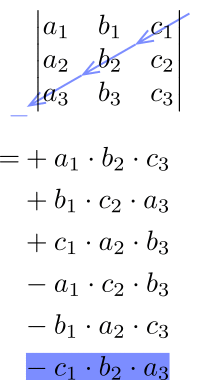
例題1
次の連立一次方程式を解け。
$$\begin{cases}\phantom{+{}}2x-2y-\phantom{1}z=4\\\phantom{+1}x-2y-2z=1\\-\phantom{1}x+3y+4z=1\end{cases}$$
No.1:連立一次方程式を行列の方程式で表す
\(A=\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\)、\(\vec x =\begin{pmatrix}x\\y\\z\end{pmatrix}\)、\(\vec b=\begin{pmatrix}4\\1\\1\end{pmatrix}\) とおくと、
$$\begin{cases}\phantom{+{}}2x-2y-\phantom{1}z=4\\\phantom{+1}x-2y-2z=1\\-\phantom{1}x+3y+4z=1\end{cases}$$
$$\Leftrightarrow\begin{pmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}4\\1\\1\end{pmatrix}$$
No.2:係数行列の行列式を計算する
$$|A|=\begin{vmatrix}2 & -2 & -1 \\1 & -2 & -2\\-1 & 3 & 4\end{vmatrix}=-1$$
No.3:求めたい変数を選ぶ
ここでは例として \(x\) を選ぶ。

No.4:選んだ変数に対応する係数行列の列を列ベクトルに置き換えた行列を用意する
No.3で1番目の変数 \(x\) を選んだため、係数行列の第1列を列ベクトル \(\vec b\) に置き換える。
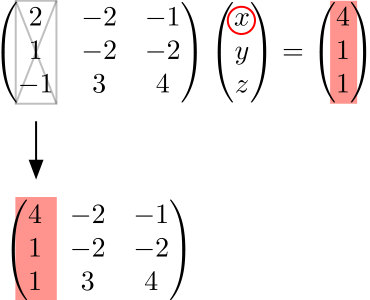
No.5:No.4の行列式を計算し、No.2で割って変数を求める
No.2より \(|A|=-1\) であるため、
$$x=\frac{\begin{vmatrix}4 & -2 & -1 \\1 & -2 & -2\\1 & 3 & 4\end{vmatrix}}{|A|}=\frac{-1}{-1}=1$$
No.6:No.3〜No.5を繰り返す
$$y=\frac{\begin{vmatrix}2 & 4 & -1 \\1 & 1 & -2\\-1 & 1 & 4\end{vmatrix}}{|A|}=\frac{2}{-1}=-2$$
$$z=\frac{\begin{vmatrix}2 & -2 & 4 \\1 & -2 & 1\\-1 & 3 & 1\end{vmatrix}}{|A|}=\frac{-2}{-1}=2$$
$$\begin{cases}x=1\\y=-2\\z=2\end{cases}$$
例題2
次の連立一次方程式を解け。
$$\begin{cases}x+2y=1\\2x+y=-7\end{cases}$$
解答
$$x=\frac{\begin{vmatrix}1 & 2 \\-7 & 1\end{vmatrix}}{\begin{vmatrix}1 & 2 \\2 & 1\end{vmatrix}}=\frac{15}{-3}=-5$$
$$y=\frac{\begin{vmatrix}1 & 1 \\2 & -7\end{vmatrix}}{\begin{vmatrix}1 & 2 \\2 & 1\end{vmatrix}}=\frac{-9}{-3}=3$$
まとめ
- クラーメルの公式を用いることで、連立一次方程式を解くことができる!
- クラーメルの公式は、変数を1つだけピンポイントで求める問題で使える!