例題を解きながら掃き出し法を用いて不定解(解が無限個)の連立一次方程式を解く方法をコツを交えながらわかりやすく解説します。
掃き出し法とは
掃き出し法とは、連立一次方程式を解くための方法の1つである。
これは、連立一次方程式に対し「基本変形」と呼ばれる同値変形を繰り返して解に相当する成分のみを残す(余計なものを掃き出す)ことで、解を求める方法になる。
掃き出し法による変形の例
$$\begin{cases}-3x_1+3x_2-2x_3+x_4-7x_5=3 \\\phantom{-}3x_1-3x_2+2x_3\phantom{{}+x_4}+9x_5=-1\\-2x_1+2x_2-\phantom{1}x_3+x_4-4x_5=2\end{cases}$$
$$\Leftrightarrow\begin{cases}x_1-x_2\phantom{{}+x_3}\phantom{{}+x_4}+3x_5 =1\\\phantom{x_1}\phantom{{}+x_2}\phantom{{}+{}}x_3\phantom{{}+x_4}\phantom{{}+0x_5} =-2\\\phantom{x_1}\phantom{{}+x_2}\phantom{{}+x_3}\phantom{{}+{}}x_4+2x_5=2\end{cases}$$
- 1つの式を何倍かする。(0倍以外)
- 2つの式を入れ替える。
- 1つの式に他の式の何倍かを加える。(0倍以外)
解の種類
連立一次方程式は、係数行列と拡大係数行列の階数によって解の種類が3パターンに変化する。
\(n\) 変数の連立一次方程式 \(A\vec x = \vec b\) とし、拡大係数行列を \([A| \vec b]\) で表す。
- \(\mathrm{rank}\:A=\mathrm{rank}\:[A| \vec b]=n\iff\)ただ1つの解 \(\vec x\)
- \(\mathrm{rank}\:A=\mathrm{rank}\:[A| \vec b]<n\iff\)不定解 \(\vec x\)
- \(\mathrm{rank}\:A<\mathrm{rank}\:[A| \vec b]\iff\)解なし
本記事では出題されることの多い「不定解」の場合の解き方を説明する。
解き方
掃き出し法は、拡大係数行列の簡約化をすることと一緒である。
なぜなら、簡約化は「行基本変形」と言われる、連立一次方程式の係数のみを取り出して基本変形を繰り返す操作であり、掃き出し法と同じ操作をしているからである。
簡約化の例
$$\left(\begin{array}{ccccc|c}-3 & 3 & -2 & 1 & -7 & 3\\3 & -3 & 2 & 0 & 9 & -1\\-2 & 2 & -1 & 1 &-4 & 2\end{array}\right)$$
$$\rightarrow\left(\begin{array}{ccccc|c}1 & -1 & 0 & 0 & 3 & 1\\0 & 0 & 1 & 0 & 0 & -2\\0 & 0 & 0 & 1 & 2 & 2\end{array}\right)$$
- 1つの行を何倍かする。(0倍以外)
- 2つの行を入れ替える。
- 1つの行に他の行の何倍かを加える。(0倍以外)
例題
次の連立一次方程式を解け。
$$\begin{cases}-3x_1+3x_2-2x_3+x_4-7x_5=3 \\\phantom{-}3x_1-3x_2+2x_3\phantom{{}+x_4}+9x_5=-1\\-2x_1+2x_2-\phantom{1}x_3+x_4-4x_5=2\end{cases}$$
No.1:連立一次方程式を行列の方程式で表す
\(A=\begin{pmatrix}-3 & 3 & -2 & 1 & -7 \\3 & -3 & 2 & 0 & 9\\-2 & 2 & -1 & 1 &-4\end{pmatrix}\)、\(\vec x =\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{pmatrix}\)、\(\vec b=\begin{pmatrix}3\\-1\\2\end{pmatrix}\) とおくと、
$$\begin{cases}-3x_1+3x_2-2x_3+x_4-7x_5=3 \\\phantom{-}3x_1-3x_2+2x_3\phantom{{}+x_4}+9x_5=-1\\-2x_1+2x_2-\phantom{1}x_3+x_4-4x_5=2\end{cases}$$
$$\Leftrightarrow\begin{pmatrix}-3 & 3 & -2 & 1 & -7 \\3 & -3 & 2 & 0 & 9\\-2 & 2 & -1 & 1 &-4\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{pmatrix}=\begin{pmatrix}3\\-1\\2\end{pmatrix}$$
No.2:拡大係数行列を求める
$$[A|\vec b]=\left(\begin{array}{ccccc|c}-3 & 3 & -2 & 1 & -7 & 3\\3 & -3 & 2 & 0 & 9 & -1\\-2 & 2 & -1 & 1 &-4 & 2\end{array}\right)$$
No.3:拡大係数行列を簡約化する
$$\left(\begin{array}{ccccc|c}-3 & 3 & -2 & 1 & -7 & 3\\3 & -3 & 2 & 0 & 9 & -1\\-2 & 2 & -1 & 1 &-4 & 2\end{array}\right)$$
$$\rightarrow\left(\begin{array}{ccccc|c}1 & -1 & 0 & 0 & 3 & 1\\0 & 0 & 1 & 0 & 0 & -2\\0 & 0 & 0 & 1 & 2 & 2\end{array}\right)$$

No.4:解の種類を確認する
簡約化の結果から、係数行列と拡大係数行列の階数がともに3であることがわかる。
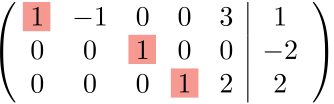
一方で変数の個数が \(x_1,\cdots,x_5\) の5個であるため、
$$\mathrm{rank}\:A=\mathrm{rank}\:[A| \vec b]=3<5$$
となり、解の種類は不定解であることがわかる。
変数の個数に対し、有効な方程式の個数が少ないと解が1つに定まらない。
また、係数行列の簡約化が単位行列 \(E\) にならないときは、解が1つに定まらないと言える。
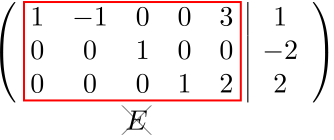
No.5:簡約化した拡大係数行列を連立一次方程式に戻す
$$\begin{pmatrix}1 & -1 & 0 & 0 & 3\\0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 1 &2\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{pmatrix}=\begin{pmatrix}1\\-2\\2\end{pmatrix}$$
$$\Leftrightarrow\begin{cases}x_1-x_2\phantom{{}+x_3}\phantom{{}+x_4}+3x_5 =1\\\phantom{x_1}\phantom{{}+x_2}\phantom{{}+{}}x_3\phantom{{}+x_4}\phantom{{}+0x_5} =-2\\\phantom{x_1}\phantom{{}+x_2}\phantom{{}+x_3}\phantom{{}+{}}x_4+2x_5=2\end{cases}$$
No.6:連立一次方程式の先頭以外の変数を任意定数に置き換える
解が1つに定まらないため、不足している分を任意定数にする。
ここでは、任意定数 \(c_1,c_2\) を自分で仮定して \(x_2=c_1\)、\(x_5=c_2\) とおく。
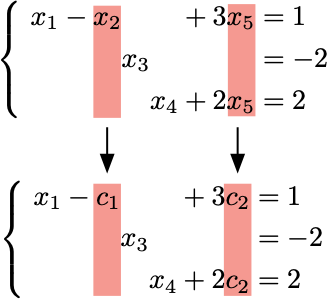
No.7:任意定数を移行して、解を求める
\(\begin{cases}x_2=c_1\\x_5=c_2\end{cases}\) かつ \(\begin{cases}x_1=1+c_1-3c_2\\x_3=-2\\x_4=2-2c_2\end{cases}\)
\(\begin{cases}x_1=1+c_1-3c_2\\x_2=c_1\\x_3=-2\\x_4=2-2c_2\\x_5=c_2\end{cases}\) (\(c_1,c_2\):任意定数)
まとめ
- 連立一次方程式の拡大係数行列を簡約化することで解が求められる!
- 変数の個数に対し、有効な方程式の個数が少ないと解が1つに定まらない!