一次結合と行列｜単位の密林

線形空間を考える上で基本となる一次結合について定義を説明し、アニメーションを用いて行列による一次結合の記法をわかりやすく示します。

一次結合とは？
内積による一次結合の記法
行列による一次結合の記法
一次結合によるベクトルの変換
例題
まとめ

一次結合とは？

一次結合（線形結合）とは、ベクトル $\vec u$ を、同じ次数の任意のベクトルの組 $\{\vec u_1,\cdots,\vec u_m\}$ を用いて

$\vec u = c_1\vec u_1+\cdots+c_n\vec u_m$ （$c_1,\cdots,c_m$は定数）

のようにそれぞれ定数倍し、足し合わせて表すことである。

（例1）$\vec u=\begin{pmatrix}-1\\3\end{pmatrix}$、$\vec u_1=\begin{pmatrix}1\\0\end{pmatrix}$、$\vec u_2=\begin{pmatrix}0\\1\end{pmatrix}$

$$\vec u = (-1)\cdot\vec u_1+3\cdot\vec u_2$$

（例2）$\vec u=\begin{pmatrix}-1\\1\end{pmatrix}$、$\vec u_1=\begin{pmatrix}1\\2\end{pmatrix}$、$\vec u_2=\begin{pmatrix}0\\-1\end{pmatrix}$

$$\vec u = (-1)\cdot\vec u_1+(-3)\cdot\vec u_2$$

内積による一次結合の記法

一次結合は内積により以下のように表記ができる。そうすることで、ベクトルと係数の部分を分離することができる。

$$c_1\vec u_1+\cdots+c_m\vec u_m=\begin{pmatrix}\vec u_1&\cdots&\vec u_m\end{pmatrix}\begin{pmatrix}c_1\\\vdots\\c_m\end{pmatrix}$$

（例）3つのベクトルの一次結合

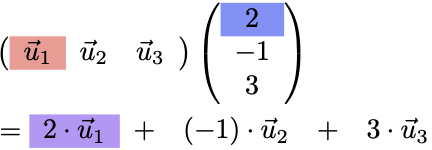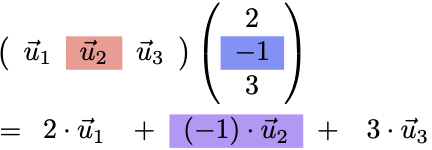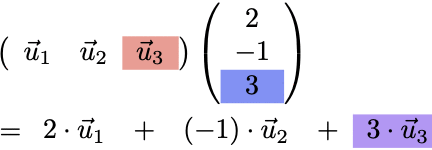
通常、線形代数では列ベクトルを考えるため、ベクトルが左、係数が右になる。

行列による一次結合の記法

ベクトルの組 $\{\vec u_1,\cdots,\vec u_m\}$ を用いた一次結合を $n$ 個用意したい場合は、上記の内積による記法を拡張するために行列を用いればよい。

具体的には、$m\times n$ 行列 $A$ を用いて以下のように表記できる。

$$\begin{eqnarray}&&\begin{pmatrix}a_{11}\vec u_1+\cdots+a_{m1}\vec u_m &\cdots& a_{1n}\vec u_1+\cdots+a_{mn}\vec u_m\end{pmatrix}\\&=&\begin{pmatrix}\vec u_1&\cdots&\vec u_m\end{pmatrix}\begin{pmatrix}a_{11} & \cdots & a_{1n}\\\vdots && \vdots\\ a_{m1} & \cdots & a_{mn}\end{pmatrix}\\&=&\begin{pmatrix}\vec u_1&\cdots&\vec u_m\end{pmatrix}A\end{eqnarray}$$

（例）2つのベクトルの一次結合を3つ

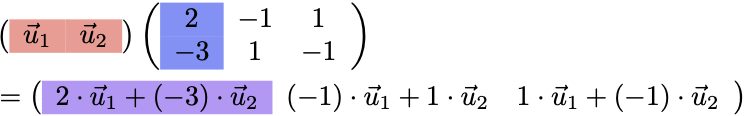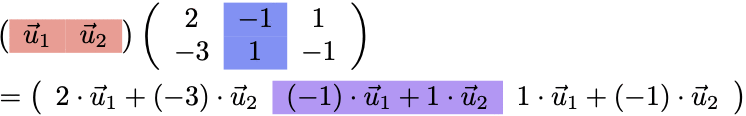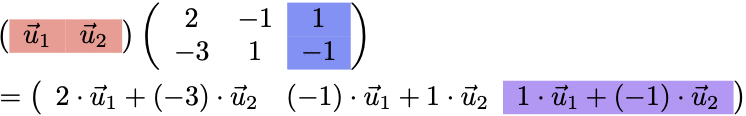
一次結合を表す場合、ベクトルの組の右から行列をかけよう！

$$\begin{pmatrix}\vec u_1&\cdots&\vec u_m\end{pmatrix}A$$

一次結合によるベクトルの変換

以上のことを使うと、$n$ 個のベクトルの組 $\{\vec v_1,\cdots,\vec v_n\}$ を、$m$ 個のベクトルの組 $\{\vec u_1,\cdots,\vec u_m\}$ の一次結合で表すには $m\times n$ 行列 $A$ を以下のように用いればよいことがわかる。

$$\begin{pmatrix}\vec v_1&\cdots&\vec v_n\end{pmatrix}=\begin{pmatrix}\vec u_1&\cdots&\vec u_m\end{pmatrix}A$$

（例）$\{\vec v_1,\vec v_2,\vec v_3\}$ を $\{\vec u_1,\vec u_2\}$ の一次結合で表す

$$\begin{eqnarray}\vec v_1&=&2\vec u_1-3\vec u_2\\\vec v_2&=&-\vec u_1+\vec u_2\\\vec v_3&=&\vec u_1-\vec u_2\end{eqnarray}$$

$$\begin{pmatrix}\vec v_1&\vec v_2 & \vec v_3\end{pmatrix}=\begin{pmatrix}\vec u_1&\vec u_2\end{pmatrix}\begin{pmatrix}2 & -1 & 1\\-3 & 1 & -1\end{pmatrix}$$

例題

次のベクトル $\{\vec v_1,\vec v_2,\vec v_3\}$ を行列を用いて $\{\vec u_1,\vec u_2,\vec u_3, \vec u_4\}$ の一次結合で表せ。

$$\begin{eqnarray}\vec v_1&=&\vec u_1+3\vec u_2-2\vec u_3+\vec u_4\\\vec v_2&=&2\vec u_2+\vec u_3\\\vec v_3&=&-3\vec u_1+4\vec u_2+2\vec u_3\end{eqnarray}$$

解答

$$\vec v_1=\begin{pmatrix}\vec u_1&\vec u_2&\vec u_3&\vec u_4\end{pmatrix}\begin{pmatrix}1\\3\\-2\\1\end{pmatrix}$$

$$\vec v_2=\begin{pmatrix}\vec u_1&\vec u_2&\vec u_3&\vec u_4\end{pmatrix}\begin{pmatrix}0\\2\\1\\0\end{pmatrix}$$

$$\vec v_3=\begin{pmatrix}\vec u_1&\vec u_2&\vec u_3&\vec u_4\end{pmatrix}\begin{pmatrix}-3\\4\\2\\0\end{pmatrix}$$

よって、

$$\begin{pmatrix}\vec v_1&\vec v_2&\vec v_3\end{pmatrix}=\begin{pmatrix}\vec u_1&\vec u_2&\vec u_3&\vec u_4\end{pmatrix}\begin{pmatrix}1 & 0 & -3\\3 & 2 & 4\\-2&1&2\\1&0&0\end{pmatrix}$$