アニメーションを用いて初学者が苦手とする行列の積(掛け算)を例題を解きながら視覚的に分かりやすく解説します。行列の積は行列の基本的な演算の1つであり、線形代数において重要です。
行列の積の定義・性質
行列の積 \(AB\) は、\(m\times \color{red}{n}\) 行列と \( \color{red}{n}\times r\) 行列のように、\(A\) の列数と \(B\) の行数が等しいときのみ定義される。
すなわち、\(A\) の列数と \(B\) の行数で「しりとり」が成立している必要がある。
- \(2\times \color{red}{2}\) 行列と \( \color{red}{2}\times 3\) 行列
- \(2\times \color{red}{3}\) 行列と \( \color{red}{3}\times 3\) 行列
- \(3\times \color{red}{3}\) 行列と \( \color{red}{3}\times 1\) 行列
最終的に、\(\color{red}{m}\times n\) 行列と \( n\times \color{red}{r}\) 行列の積は、\(\color{red}{m}\times \color{red}{r}\) 行列になる。
- \(\color{red}{2}\times 2\) 行列と \( 2\times \color{red}{3}\) 行列の積→ \(\color{red}{2}\times \color{red}{3}\) 行列
- \(\color{red}{2}\times 3\) 行列と \( 3\times \color{red}{3}\) 行列の積→ \(\color{red}{2}\times \color{red}{3}\) 行列
- \(\color{red}{3}\times 3\) 行列と \( 3\times \color{red}{1}\) 行列の積→ \(\color{red}{3}\times \color{red}{1}\) 行列
解き方
行列の積は、行ベクトルと列ベクトルの内積を規則に沿って書き並べることで求められる。
例題
次の計算をせよ。
$$\begin{pmatrix}1 & 3 & -2 \\-1 & 5 & 4\end{pmatrix}\begin{pmatrix}3 & -2 & 4 \\-4 & 1 & 2 \\ 2 & 3 & -1\end{pmatrix}$$
No.1:行列 \(A\)、\(B\) に「行」「列」に従って線を入れる
行列のかけ算は「行」\(\times\)「列」で計算する。

No.2:\(A\) の行ベクトル、\(B\) の列ベクトルをそれぞれ1つずつ選ぶ
ここでは例として1行目と1列目を選ぶ。

No.3:選んだ2つのベクトルの内積を計算する
内積は、お互いの対応する成分の積を合計することで求められる。
$$\begin{align*}&\begin{pmatrix} 1 & 3 & -2\end{pmatrix}\begin{pmatrix} 3 \\ -4 \\ 2 \end{pmatrix}\\&=1\cdot3+3\cdot(-4)+(-2)\cdot2\\&=-13\end{align*}$$
No.4:選んだ \(A\) の行ベクトルの「行」、\(B\) の列ベクトルの「列」の位置に、内積の結果を配置する
ここでは、\(A\) の行ベクトルが1行目、\(B\) の列ベクトルが1列目なので、\((1,1)\) 成分に内積の結果を配置している。

No.5:No.2〜No.4を繰り返す
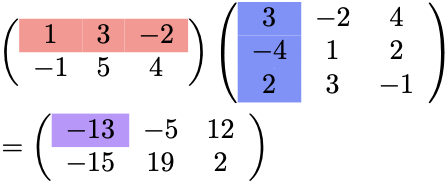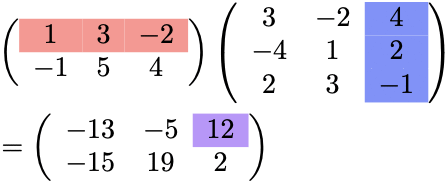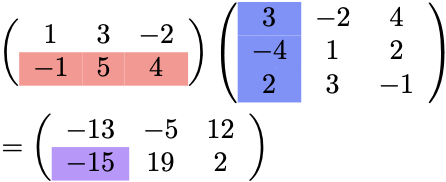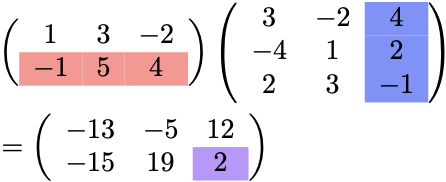
最終的に、\(\color{red}{2}\times 3\) 行列と \( 3\times \color{red}{3}\) 行列の積なので、 \(\color{red}{2}\times \color{red}{3}\) 行列になっている。
すなわち、\(2\times3=6\) 回も内積を計算する必要がある…

$$\begin{pmatrix}-13 & -5 & 12 \\-15 & 19 & 2\end{pmatrix}$$
まとめ
- 行列の積が定義できるのはしりとりが成り立つときのみ!
- 行列のかけ算は「行」\(\times\)「列」で計算!
考え方のイメージ
行列は行や列に区切るとベクトルの集合になる。
すなわち、行列の構成単位はベクトルなのである。
従って、行列の積の成分は、単純な成分同士の積ではなく、行ベクトルと列ベクトルの内積になっている。