余因子展開と行列式

アニメーションを用いて余因子展開で行列式を求める方法を例題を解きながら視覚的にわかりやすく解説します。余因子展開は行列式の計算を楽にするための基本テクニックです。

余因子展開とは？
余因子展開を使うメリット
例題
まとめ

余因子展開とは？

余因子展開とは、行列式の1つの行（または列）に注目して、一回り小さな行列式の足し合わせに展開するテクニックである。

（例）第1行に関する余因子展開

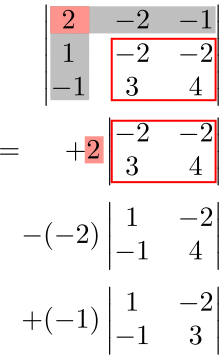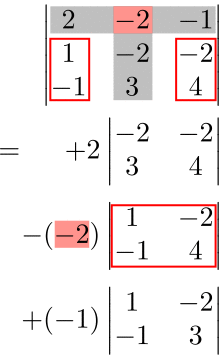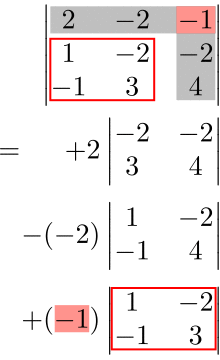
ここで、余因子展開の足し合わせの符号は以下の法則によって決められる。

$(i,j)$ 成分に注目しているとき、$(-1)^{i+j}$ が足し合わせの符号になる。

$(1,1)$ 成分→ $(-1)^{1+1}=(-1)^2=+1$
$(1,2)$ 成分→ $(-1)^{1+2}=(-1)^3=-1$
$(1,3)$ 成分→ $(-1)^{1+3}=(-1)^4=+1$

上の符号法則を表にした「符号表」を書くと分かりやすい。

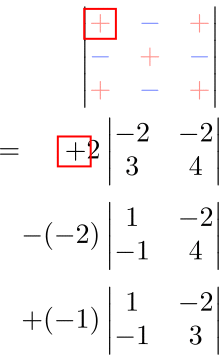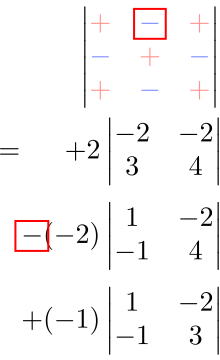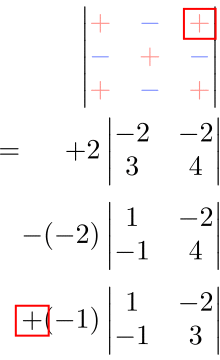
余因子展開は、別の行（または列）を選んでも同じ答えになる。

（例）第2列に関する余因子展開

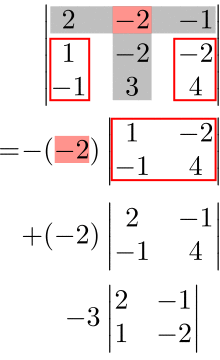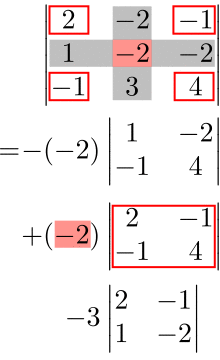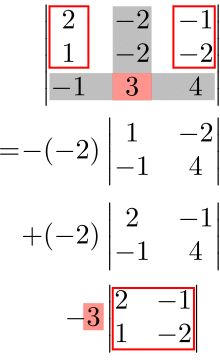
余因子展開を使うメリット

余因子展開を使うメリットは、

サラスの方法と違い、どのような大きさの行列式でも使える
次数の1つ小さな行列式で計算できる
行列の成分に0が多いとき、計算を楽にできる

などが挙げられる。

行列の成分に0が多いときは余因子展開を使おう！

例題

次の行列式を求めよ。

$$\begin{vmatrix} 1 & -1 & 2 & 1\\0 & 0 & 3 & 0 \\-3 & 2 & -2 & 2 \\-1 & 0 & 1 & 0\end{vmatrix}$$

No.1：注目する行（列）を1つ選ぶ

ここでは、成分に0の多い第2行に注目する。

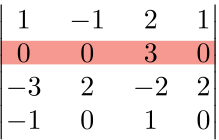
No.2：注目している行（列）の成分を1つ選ぶ

ここでは $(2,1)$ 成分を選ぶ。

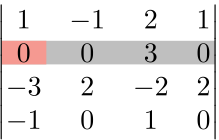
No.3：余因子展開の符号を決める

ここでは $(2,1)$ 成分を選んでいることから、$-1$ を $2+1=3$ 乗する。

$$(-1)^{2+1}=(-1)^3=-1$$

または、符号表を書いてからマイナスと求めてもよい。

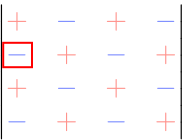
No.4：成分に対応する行・列を除いて一回り小さな行列式を作る

ここでは、 $(2,1)$ 成分を選んでいることから、第2行と第1列を除いた行列式を作る。

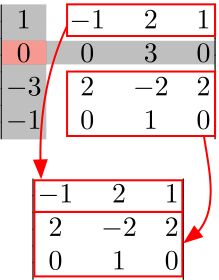
No.5：No.2〜No.4を掛け合わせる

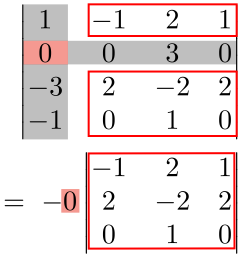
No.6：No.2〜No.5を繰り返して足し合わせる

成分0の項は消えるため、計算を省略してもよい。

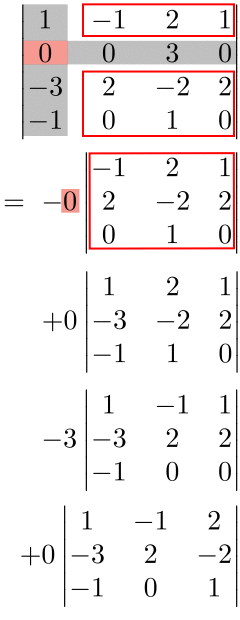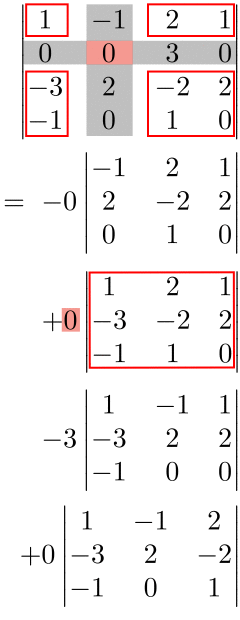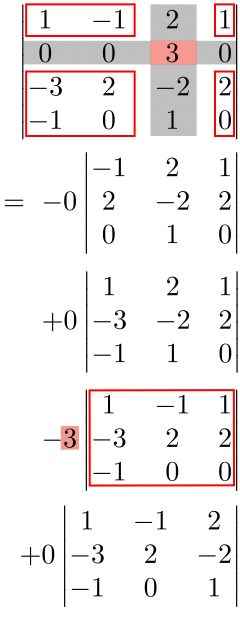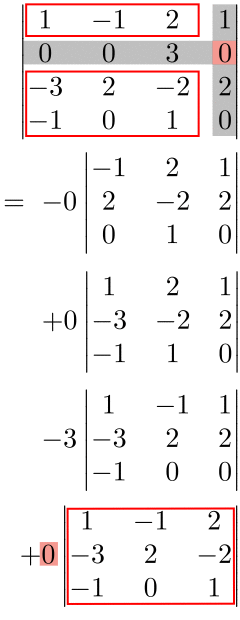
小行列式でも余因子展開を行えばさらに楽ができる。

$$\begin{align*}\begin{vmatrix} 1 & -1 & 2 & 1\\0 & 0 & 3 & 0 \\-3 & 2 & -2 & 2 \\-1 & 0 & 1 & 0\end{vmatrix}&=-3\begin{vmatrix} 1 & -1 & 1\\-3 & 2 & 2 \\-1 & 0 & 0\end{vmatrix}\\&=-3\cdot(-1)\begin{vmatrix}-1 & 1\\ 2 & 2 \end{vmatrix}\\&=-3\cdot(-1)\cdot\{(-1)\cdot 2-1\cdot 2\}\\&=-12\end{align*}$$

答え

$$-12$$