ベクトル解析分野の存在意義
私たちがいる3次元空間において、物体を押す”方向”、電気力線の”方向”といったように「向き」を考慮しないと身の回りの現象を説明することは出来ない。
これら3次元的な現象を説明する数学分野が「ベクトル解析」である。
例えば、運動の第2法則は高校物理では
$$ma=F$$
と学んだ。ここで、加速度 \(a\) と 力 \(F\) は「向き」の概念を持つので
$$m\vec{a}=\vec{F}$$
とベクトルを使って書き直される。このベクトルを使った式を自由に使いこなすことがベクトル解析分野の目標である。
大学におけるベクトル表記
高校数学では 「\(A\) ベクトル」を \(\vec{A}\) と上付き矢印で表現していたが、
大学の講義や文献においては太字の\(A\)、
すなわち\(\mathbb{A}\) や \(\pmb{A}\) で書くことが多い。
矢印を書くのがめんどくさい。ベクトルだらけになった時に矢印で数式が埋め尽くされてしまう。といったところが主な理由である。
このベクトル解析の記事でも基本的には 「\(A\) ベクトル」を太字 \(\pmb{A}\) で書くことにする。
例えば、先ほどの運動の第2法則は
$$m\pmb{a}=\pmb{F}$$
と書く。
大学におけるベクトル成分表記
\(xyz\) 空間上にて \(x\) 成分が \(2\) , \(y\) 成分が \(3\) , \(z\) 成分が \(5\) の点 \(A\) はもちろん
$$A=\left(2,3,5\right)$$
と書く。また、点 \(A\) の位置ベクトル \(\vec{OA}\) は
$$\vec{OA}=\left(2,3,5\right)$$
と書く。
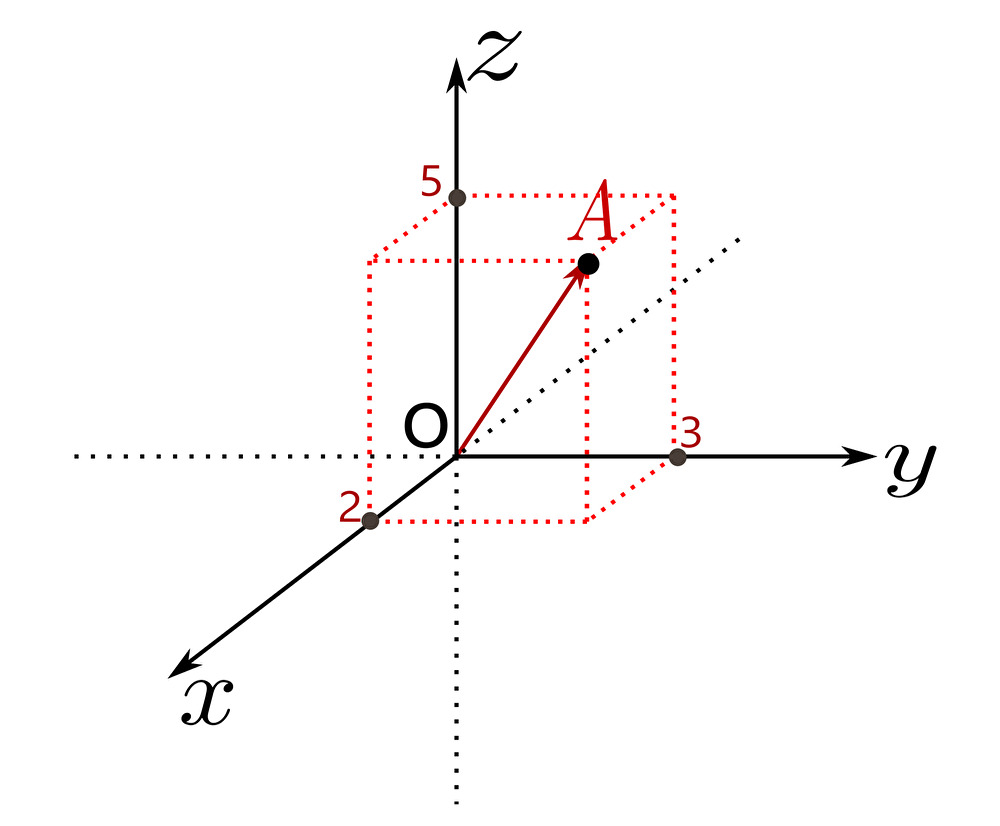
ここで、各軸方向の単位ベクトル \(\pmb{i}=\left(1,0,0\right)\), \(\pmb{j}=\left(0,1,0\right)\), \(\pmb{k}=\left(0,0,1\right)\) を用いて位置ベクトル \(\vec{OA}\) は
\begin{eqnarray}\vec{OA}&=&\left(2,0,0\right)+\left(0,3,0\right)+\left(0,0,5\right)\\\\&=&2\times\left(1,0,0\right)+3\times\left(0,1,0\right)+5\times\left(0,0,1\right)\\\\&=&2\pmb{i}+3\pmb{j}+5\pmb{k}\end{eqnarray}
と書くことができる。
このように全てのベクトル \(\left(a,b,c\right)\) はこの基本ベクトル \(\pmb{i}=\left(1,0,0\right)\), \(\pmb{j}=\left(0,1,0\right)\), \(\pmb{k}=\left(0,0,1\right)\) を用いて
$$\left(a,b,c\right)=a\pmb{i}+b\pmb{j}+c\pmb{k}$$
と表現することができる。数式で使われる括弧とベクトル成分表示の括弧が混同することを嫌う人はこの基本ベクトルを用いた成分表示を行うといい。
基本ベクトル \(\pmb{i}\), \(\pmb{j}\), \(\pmb{k}\) についてだが \(\pmb{e_{x}}\), \(\pmb{e_{y}}\) ,\(\pmb{e_{z}}\) と書く流派もある。
まとめ
・ベクトルは太字で書くことが多い。(矢印を上付きで書くのがめんどくさいので)
・基本ベクトル \(\pmb{i}\), \(\pmb{j}\), \(\pmb{k}\) を用いて成分表示する手法もある。(数式の括弧とベクトル成分表示の括弧が混同するのが嫌な人用。ちなみに結構使われている。)