1階線形常微分方程式

1階線形微分方程式
例題
例題の解答
練習問題
ひとこと

1階線形微分方程式

次の形の微分方程式を考えよう。( $p(x),q(x)$ は $x$ だけの関数とする。)

$$y’+p(x)y=q(x)$$

この形の微分方程式は $p(x)y$ の項が邪魔で左辺右辺それぞれに上手く「$x$だけの式」と「$y$だけの式」に整理することができない。

よって変数分離の解法とはまた別の戦法で解き進める必要がある。

例題

上式における　$p(x)=1,　q(x)=\cos{x}$ の場合

つまり、次の微分方程式を解け。　$$y’+y=\cos{x}$$　

例題の解答

No.1　:　左辺をムリヤリ積の微分形に変形

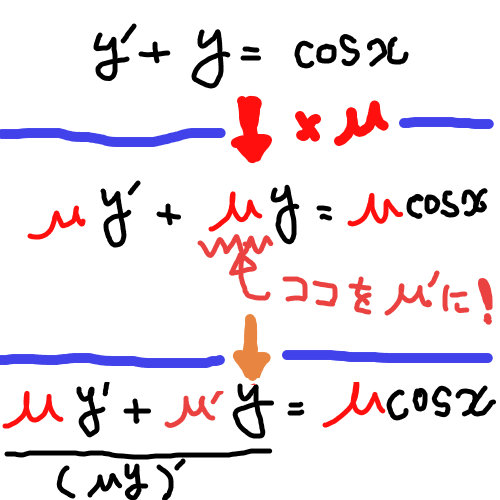
まず両辺に $x$ の関数 $\mu(x)$ をかける。

$$\mu y’+\mu y=\mu\cdot\cos{x}$$

ここで、$\mu$ について $\mu=\mu’$ を満たすものと設定すれば

左辺第二項目を置き換えた次の式を得る。

$$\mu y’+\mu’ y=\mu\cdot\cos{x}$$

$\mu y’+\mu y=\mu\cdot\cos{x}$ の左辺について、$\mu y’+\mu’ y=\left(\mu\cdot y\right)’$ を連想した。

さらに左辺について $\left(\mu\cdot y\right)’=\mu y’+\mu’ y$ より

$$\left(\mu\cdot y\right)’=\mu\cdot\cos{x}$$

今、$\mu$ について $\mu=\mu’$ と設定したが、これはつまり $\mu(x)=\mathrm{e}^x$ ということ（微分しても形が変わらない関数）だから

$$\left(\mathrm{e}^x\cdot y\right)’=\mathrm{e}^x\cdot\cos{x}\cdot\cdot\cdot\left(A\right)$$

と変形できる。

このムリヤリ設定した $\mu$ を積分因子という。

$\mu=\mu’$ から $\mu=\mathrm{e}^x$ を得たが、このとき積分定数がいらないことに注意!!

$\mu=\mathrm{e}^x+C$ としないこと!!

No.2　:　両辺を $x$ で積分

$\left(A\right)$ 式の両辺を $x$ で積分する。

$$\mathrm{e}^x\cdot y=\int\left(\mathrm{e}^x\cdot\cos{x}\right)dx\cdot\cdot\cdot\left(B\right)$$

右辺の積分について

$$\int\left(\mathrm{e}^x\cdot\cos{x}\right)dx=\displaystyle\frac{1}{2}\mathrm{e}^x\left(\sin{x}+\cos{x}\right)+C\ \ \ \left(Cは積分定数\right)$$

であるので $\left(B\right)$ 式は

$$\mathrm{e}^x\cdot y=\displaystyle\frac{1}{2}\mathrm{e}^x\left(\sin{x}+\cos{x}\right)+C$$

両辺を $\mathrm{e}^x$ で割ると

$$y=\displaystyle\frac{1}{2}\ \left(\sin{x}+\cos{x}\right)+C\mathrm{e}^{-x}$$

練習問題

練習問題1

$$y’-y=x$$

練習問題2

$$y’+2xy=x$$

練習問題3

$$y’+3y=\mathrm{e}^{3x}$$

練習問題4

$$xy’+2y=\cos{x}$$

練習問題5

$$\left(x^2\sin{x}-y\right)dx+xdy=0$$

ひとこと

今回の微分方程式では 積の微分形 を利用して解き進めていった。

$\left(\mu(x)y(x)\right)’=\mu'(x)y(x)+\mu(x)y'(x)$ の関係式を適用させるために両辺に $\mu$ をかけて $y$ の係数が $\mu’$ となるように設定を与える。(例題では $y$ の係数が $\mu$ であるので $\mu=\mu’$ と設定する。)