右辺が0でない2階線形微分方程式
次の形の微分方程式を考えてみよう。
$$y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)$$
右辺が0のときの解法は下記事にて説明した。
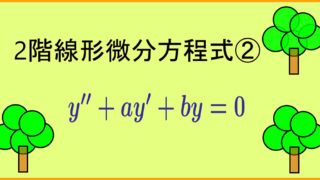
今回はその応用として右辺に \(x\) の関数 \(f(x)\) が追加されたときの解法について説明する。
例題
微分方程式 \(y^{\prime\prime}-7y^{\prime}+12y=12x^2+10x\) を解け。
例題の解答
No.1 : 右辺を0として微分方程式を解く
微分方程式 \(y^{\prime\prime}-7y^{\prime}+12y=12x^2+10x\) の右辺を0とした式 $$y^{\prime\prime}-7y^{\prime}+12y=0\cdot\cdot\cdot\left(A\right)$$ を解く。まず、式 \(\left(A\right)\) の特性方程式を解くと $$\lambda^2-7\lambda+12=0$$ $$\left(\lambda-3\right)\left(\lambda-4\right)=0$$ $$\lambda=\begin{cases}3\\4\end{cases}$$ 従って、右辺を0とした式 \(\left(A\right)\) の解 \(y_0\) は定数 \(C_1\)、\(C_2\) を用いて $$y_0=C_1\mathrm{e}^{3x}+C_2\mathrm{e}^{4x}$$ と表される。
この右辺を0に塗り替えた微分方程式の解 \(y_0\) を \(y^{\prime\prime}-7y^{\prime}+12y=0\) の一般解という。
No.2 : 右辺の関数の形から解となる関数を予想し代入
今回の微分方程式の右辺の関数は、2次関数 \(12x^2+10x\) であるので、解となる関数を二次関数 \(y=px^2+qx+r\) と予想する。
このとき、\(y’=2px+q\) と \(y^{\prime\prime}=2p\) を得る。
これを微分方程式 \(y^{\prime\prime}-7y^{\prime}+12y=12x^2+10x\) の左辺に代入して \begin{eqnarray}(左辺)&=&y^{\prime\prime}-7y^{\prime}+12y\\\\&=&(2p)-7(2px+q)+12(px^2+qx+r)\\\\&=&(12p)x^2+(12q-14p)x+(2p-7q+12r)\end{eqnarray}
すなわち
$$(12p)x^2+(12q-14p)x+(2p-7q+12r)=12x^2+10x$$
となる。両辺の係数を比較して
$$\begin{cases}12p=12\\12q-14p=10\\2p-7p+12r=0\end{cases}$$
ここから
$$\begin{cases}p=1\\q=2\\r=1\end{cases}$$
を得る。従って、\(y_p=x^2+2x+1\) は解であることがわかる。
このような右辺の関数の形から解となる関数の形を予想し、代入することで導かれる解 \(y_p\) を \(y^{\prime\prime}-7y^{\prime}+12y=12x^2+10x\) の特殊解という。
No.3 : No.1で得た 一般解 \(y_0\)とNo.2で得た 特殊解 \(y_p\) を合体させて真の解を導く
求める微分方程式の解 \(y\) は No.1で得た 一般解 \(y_0\) とNo.2で得た 特殊解 \(y_p\) の和で得られる。
最終的な微分方程式の解が一般解 \(y_0\) と 特殊解 \(y_p\) の和で与えられる理由について説明する。
微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) を考える。
右辺を0とした微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=0\) は特性方程式を用いることで解くことができ、その解を \(y_0\) とする。この \(y_0\) は定数 \(C_1\)、\(C_2\) を含んでおり微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=0\) のすべての解を表している。このことから \(y_0\) は \(y^{\prime\prime}+ay^{\prime}+by\) \(=0\) の一般解と呼ぶ。
一方で、微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の右辺から関数の形を予想して得た解 \(y_p\) は \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の一つの解に過ぎない。このことから \(y_p\) は \(y^{\prime\prime}+ay^{\prime}+by\) \(=f\left(x\right)\) の特殊解と呼ぶ。
最終的に求める微分方程式の解、すなわち微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の解すべてを表現できる解(一般解)を \(Y\) として、\(Y=y_0+y_p\) とおくと、
\begin{eqnarray}&&Y^{\prime\prime}+aY^{\prime}+bY\\\\&=&\left(y_0+y_p\right)^{\prime\prime}+a\left(y_0+y_p\right)^{\prime}+b\left(y_0+y_p\right)\\\\&=&y^{\prime\prime}_0+y^{\prime\prime}_p+ay^{\prime}_0+ay^{\prime}_p+by_0+by_p\\\\&=&\left(y^{\prime\prime}_0+ay^{\prime}_0+by_0\right)+\left(y^{\prime\prime}_p+ay^{\prime}_p+by_p\right)\end{eqnarray}
ここで、\(y_0\) は \(y^{\prime\prime}+ay^{\prime}+by=0\) の解であり、\(y_p\) は \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) の解であるので
$$\begin{cases}y^{\prime\prime}_0+ay^{\prime}_0+by_0=0\\y^{\prime\prime}_p+ay^{\prime}_p+by_p=f\left(x\right)\end{cases}$$
が成り立つ。従って、
\begin{eqnarray}&&\left(y_0+y_p\right)^{\prime\prime}+a\left(y_0+y_p\right)^{\prime}+b\left(y_0+y_p\right)\\\\&=&\left(y^{\prime\prime}_0+ay^{\prime}_0+by_0\right)+\left(y^{\prime\prime}_p+ay^{\prime}_p+by_p\right)\\\\&=&0+f\left(x\right)\\\\&=&f\left(x\right)\end{eqnarray}
つまり、$$\left(y_0+y_p\right)^{\prime\prime}+a\left(y_0+y_p\right)^{\prime}+b\left(y_0+y_p\right)=f\left(x\right)$$ であるので、\(Y=y_0+y_p\) は 微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right) \) の解であり、定数 \(C_1\)、\(C_2\)を含むため微分方程式 \(y^{\prime\prime}+ay^{\prime}+by=f\left(x\right)\) のすべての解を表している。このことから \(y_0+y_p\) は \(\left(y_0+y_p\right)^{\prime\prime}+a\left(y_0+y_p\right)^{\prime}+b\left(y_0+y_p\right)\) \(=0\) の一般解と呼ぶ。
練習問題
練習問題1
\(y^{\prime\prime}+2y^{\prime}-3y=9x\) を解け。
練習問題2
\(y^{\prime\prime}-2y^{\prime}+2y=4x^2+2\) を解け。
練習問題3
\(y^{\prime\prime}-y^{\prime}+y=14\mathrm{e}^{3x}\) を解け。
練習問題4
\(y^{\prime\prime}-y^{\prime}+y=-17\sin{2x}\) を解け。
練習問題5
\(y^{\prime\prime}-5y^{\prime}+6y=3\sqrt{2}\ \mathrm{e}^{x}\cos{\sqrt{2}x}\) を解け。
ひとこと
2階線形微分方程式の右辺が \(x\) の関数であった場合、右辺を0とした微分方程式の一般解 \(y_0\) と 右辺の \(x\) の関数 から解を予想して得た特殊解 \(y_p\) の和が求める微分方程式の解である。






