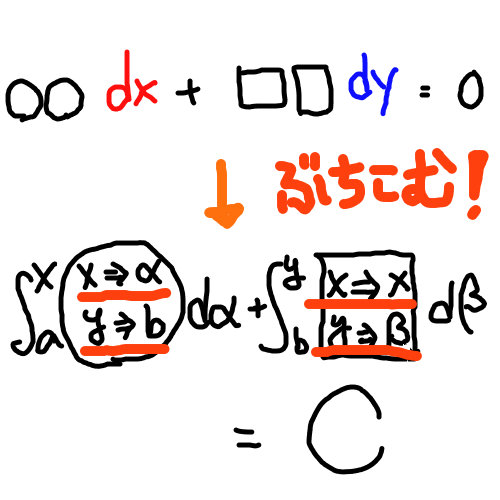完全微分方程式
次の形の微分方程式を考えてみよう。
$$2xy\ dx+\left(x^2+y\right)dy=0$$
\(x\) と \(y\) が足し算なり掛け算なりで入り混じっており変数分離はとてもできそうにない。
次に、この微分方程式が1階線形微分方程式であるかを確認する。
両辺を \(dx\) で割ると
$$2xy+\left(x^2+y\right)\displaystyle\frac{dy}{dx}=0$$
$$\left(x^2+y\right)y’+2xy=0$$
さらに、両辺を \(\left(x^2+y\right)で割って\)
$$y’+\displaystyle\frac{2x}{x^2+y}y=0$$
となり \(y\) の係数に \(y\) が含まれる( \(x\) のみでない)ので1階線形微分方程式でもないことが分かる。
今回の微分方程式もまた既知の方法以外で解いていかないといけないわけである。
さて、今回の微分方程式にはある特徴がある。
\(dx\) の係数 \(2xy\) を \(y\) について微分すると \(2x\) を得る。
\(dy\) の係数 \(\left(x^2+y\right)\) を \(x\) について微分すると \(2x\) を得る。
このように、( \(dx\) の係数の \(y\) 微分) = ( \(dy\) の係数の \(x\) 微分) となる微分方程式を 完全微分方程式 という。
この記事では 完全微分方程式 の解き方の流れを確認する。
完全微分方程式とは…
\(P(x,y)dx+Q(x,y)dy=0\) において(右辺が0であることに注意)
$$\displaystyle\frac{dP}{dy}=\displaystyle\frac{dQ}{dx}$$
を満たす微分方程式のことをいう。
解法
問題の微分方程式が 完全微分方程式 であることが確認されればやることはただ一つ
以下の式に当てはめる だけである。
$$\int^{x}_{a}P(\alpha,b)\ d\alpha+\int^{y}_{b}Q(x,\beta)\ d\beta=C\ \ \ \left(A\right)$$
ただし \(a\)、\(b\)、\(C\) は定数、\(\alpha\)、\(\beta\) は積分変数である。
例題
次の微分方程式を解け。
$$2xy\ dx+\left(x^2+y\right)dy=0$$
例題の解答
No.1 : 完全微分方程式であるか確認する
$$\displaystyle\frac{d}{dy}\left(2xy\right)=2x$$
$$\displaystyle\frac{d}{dx}\left(x^2+y\right) = 2x$$
\(\displaystyle\frac{d}{dy}\left(2xy\right)=\displaystyle\frac{d}{dx}\left(x^2+y\right)\) であるので問題の微分方程式は 完全微分方程式 である。
No.2 : 式 (A) にぶち込む
今回、\(P(x,y)=2xy\) 、\(Q(x,y)=x^2+y\) であるので、
\(P(\alpha,b)=2\alpha b\)、\(Q(x,\beta)=x^2+\beta\) となり式 \(\left(A\right)\) に代入すると
$$\int^{x}_{a}\left(2\alpha b\right)\ d\alpha+\int^{y}_{b}\left(x^2+\beta\right)\ d\beta=C$$
$$\left[\alpha^{2}b\right]^{x}_{a}+\left[x^{2}\beta+\displaystyle\frac{1}{2}\beta^{2}\right]^{y}_{b}=C$$
$$\left(x^{2}b-a^{2}b\right)+\{\left(x^{2}y+\displaystyle\frac{1}{2}y^2\right)-\left(x^{2}b+\displaystyle\frac{1}{2}b^{2}\right)\}=C$$
$$x^{2}y+\displaystyle\frac{1}{2}y^2=C+a^{2}b+\displaystyle\frac{1}{2}b^2$$
ここで、\(a\)、\(b\) が定数のため右辺 \(C+a^{2}b+\displaystyle\frac{1}{2}b^2\) は定数であり、\(C’=C+a^{2}b+\displaystyle\frac{1}{2}b^2\) とまとめてあげて
$$x^{2}y+\displaystyle\frac{1}{2}y^2=C’\ \ \ (C’は積分定数)$$
練習問題
練習問題1
$$y^{2}\ dx+2xy\ dy=0$$
練習問題2
$$y\ dx+\left(x+y\right)\ dy=0$$
練習問題3
$$\sin{x}\log{y}\ dx-\displaystyle\frac{\cos{x}}{y}\ dy=0$$
練習問題4
$$\left(2xy+\mathrm{e}^{x}\right)\ dx+\left(\mathrm{e}^{y}+x^2\right)\ dy=0$$
練習問題5
$$y’=\displaystyle\frac{\mathrm{e}^{x}\sin{y}+\mathrm{e}^{y}\sin{x}}{\mathrm{e}^{y}\cos{x}-\mathrm{e}^{x}\cos{y}}$$
ひとこと
\((\bigcirc\bigcirc dx+\bigcirc\bigcirc dy=0)\) の形は大抵この完全微分方程式形である。(練習問題4,5のように指数関数、三角関数、対数関数が複数登場している式も完全微分方程式形であることが多い。)
完全微分方程式 は式(A)に当てはめるだけで機械的な積分計算のみで答えを導くことができるため、式さえ覚えておけば安定して解くことができるようになる。(実は他に解き方はあるのだが安定性はこちらが上)