人によりしっくりくる微分演算子法
一般的に使われている微分演算子法は 微分演算子 \(D\) で書き直した微分方程式にて割り算・因数分解・部分分数分解や式変形の公式を使うこと不定積分を意味するその逆数 \(\displaystyle\frac{1}{D}\) を登場させて解いてきた。


しかし、「微分 \(\displaystyle\frac{d}{dx}\) を意味する \(D\) で割るとはこれ如何に」「公式覚えるのきつい」など人を選ぶ方法であると思う。
実は3階以上の微分方程式においても2階線形微分方程式の時と同様に、「解を予想する方法」を使うことでシンプルに微分方程式を解くことができる。
また登場!「解予想」
今回紹介する方法は次の2点で微分演算子法に対して有利である。
・計算ミスを誘発する逆演算子 \(\displaystyle\frac{1}{D}\) を一切登場しないこと
・複雑な公式暗記を必要としないこと
次の2点は留意しておこう
多くの微分方程式では特性方程式を因数分解して出てくる因数として3つのパターンがある。
- \(\left(\lambda-\alpha\right)\)
- \(\left(\lambda-\alpha\right)^{n}\)
- \(\left(\lambda^{2}+\beta^{2}\right)\)
この3つのパターンそれぞれに基本解の情報が含まれている。
3パターンの因数はそれぞれ
- \(\mathrm{e}^{\alpha x}\)
- ( \(n-1\) 次の多項式)\(\cdot\ \mathrm{e}^{\alpha x}\)
- \(\cos{\beta x}\) と \(\sin{\beta x} \)
の基本解を与える。
この解はまだ微分方程式のすべての解を表現できてない(一部の解でしかない)ので
複数の基本解 \(y_{1}\)、\(y_{2}\) が得られた場合はそれらを一次結合(定数掛け算したものどうしの和)させることで \(c_{1}y_{1}+c_{2}y_{2}\) となり、これが最終的に答えとなる解である。
\(y^{\prime\prime}-5y^{\prime}+6y=0\) は
$$\left(\lambda^{2}-5\lambda+6\right)y=0$$
$$\left(\lambda-2\right)\left(\lambda-3\right)=0$$
より、パターン1の因数を持つので、基本解は \(\mathrm{e}^{2x}\)、\(\mathrm{e}^{3x}\) であり、これらを1次結合させると一般解
$$y=C_{1}\mathrm{e}^{2x}+C_{2}\mathrm{e}^{3x}$$
を得る。
この3つのパターンについては次の記事で近しいものを扱っている。
https://jfor.net/2%E9%9A%8E%E7%B7%9A%E5%BD%A2%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B%E5%BC%8F%E2%9E%812階線形微分方程式の時と同様に右辺が0でない微分方程式においては、解の形を予想するステップも必要となる。
例えば、微分方程式
$$y^{\prime\prime\prime}-3y^{\prime}+2y=\mathrm{e}^{2x}$$
においては 右辺が指数関数 \(\mathrm{e}^{2x}\) であるので解となる関数の形は定数 \(C\) を使って
$$y=C\mathrm{e}^{2x}$$
と予想される。
\(y^{\prime\prime}-4y^{\prime}+3y=\mathrm{e}^{2x}\) は
特性方程式を解くと
$$\left(\lambda-1\right)\left(\lambda-3\right)=0$$
$$\lambda=1,3$$
従って、斉次方程式 \(y^{\prime\prime}-4y^{\prime}+3y=0\) の一般解は
$$y_{0}=C_{1}\mathrm{e}^{x}+C_{2}\mathrm{e}^{3x}$$
ここで、右辺の指数関数 \(\mathrm{e}^{2x}\) から解となる関数の形は
$$y_{p}=C\mathrm{e}^{2x}$$
と予想できる。\(x\) で1回、2回微分すると
$$y^{\prime}_{p}=2C\mathrm{e}^{2x}$$
$$y^{\prime\prime}_{p}=4C\mathrm{e}^{2x}$$
となる。元の微分方程式に代入して
$$\left(4C-8C+3C\right)\mathrm{e}^{2x}= \mathrm{e}^{2x} $$
$$C=-1$$
従って \(y_{p}=-\mathrm{e}^{2x}\)
最終的に求める真の解は一般解 \(y_{0}\) と特殊解 \(y_{p}\) の和であるので
\begin{eqnarray}y&=&y_{0}+y_{p}\\\\&=&C_{1}\mathrm{e}^{x}+C_{2}\mathrm{e}^{3x}-\mathrm{e}^{2x}\end{eqnarray}
解の形を予想して元の式に代入することで得た解 \(y_{p}\) は係数がない(定数をつけない)ことに注意!!
例題
\(y^{\prime\prime\prime}-3y^{\prime}-2y=\mathrm{e}^{-2x}\) を解け。
例題の解答
No.1 : 右辺を0として微分方程式を解く。
微分方程式 \(y^{\prime\prime\prime}-3y^{\prime}-2y=\mathrm{e}^{-2x}\) の右辺を0とした式
$$y^{\prime\prime\prime}-3y^{\prime}-2y=0\cdot\cdot\cdot\left(A\right)$$
を解く。特性方程式は
$$\lambda^{3}-3\lambda-2=0$$
多項式 \(\lambda^{3}-3\lambda-2\) に \(\lambda=-1\) を代入すると \((-1)^{3}-3\times(-1)-2=0\) となるので、\(\lambda+1\) を因数として持つことが分かる。従って、多項式どうしの割り算計算をしてあげると
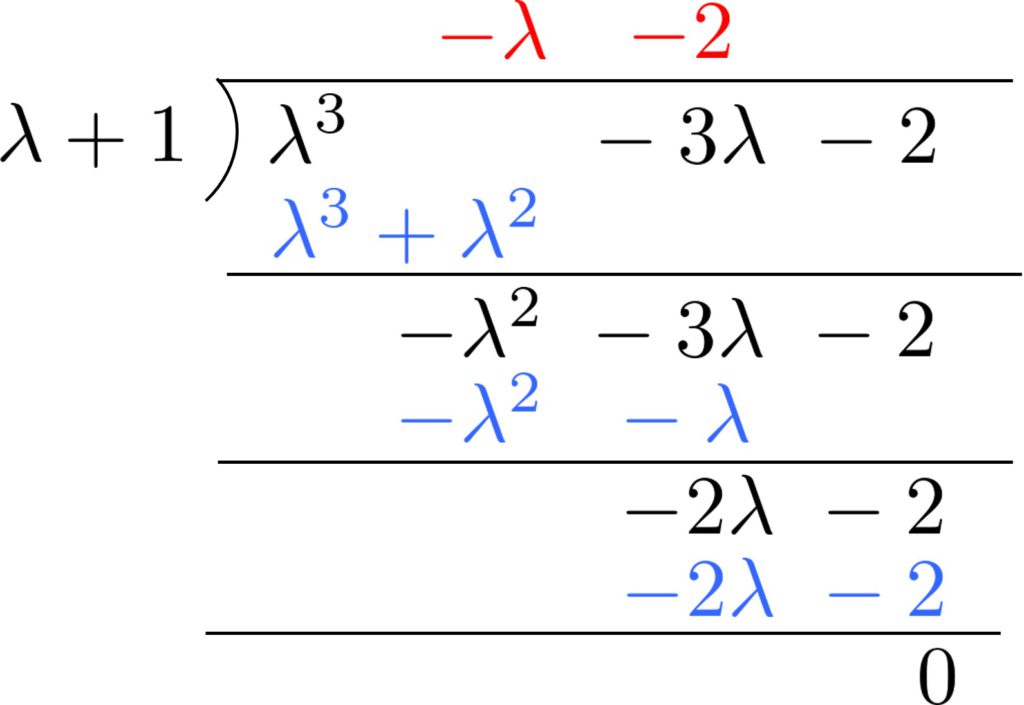
となり、
$$\left( \lambda +1\right)\left( \lambda ^{2}- \lambda -2\right)=0$$
$$ \left( \lambda +1\right) \left( \lambda +1\right) \left( \lambda -2\right) =0$$
$$ \left( \lambda +1\right)^{2} \left( \lambda -2\right)=0$$
と因数分解される。
従って、特性方程式を解くと \(\lambda=-1\) (重解)、\(\lambda=2\) となり、式(A)の一般解 \(y_{0}\) は定数 \(C_{1}\)、\(C_{2}\)、\(C_{3}\) を用いて
$$y_{0}=\left(C_{1}+C_{2}x\right)\mathrm{e}^{-x}+C_{3}\mathrm{e}^{2x}$$
となる。
特性方程式が重解を持つときは指数関数の係数が定数係数のべき乗関数となることに注意!!今回は \(\lambda=-1\) が 2重解 であるので (2-1)=1 次関数が係数となる。
No.2 : 右辺の関数の形から解となる関数を予想して代入
今回の微分方程式の右辺の関数は指数関数 \(\mathrm{e}^{-2x}\) であるので、解となる関数を定数 \(C\) を用いて \(y_{p}=C\mathrm{e}^{-2x}\) と予想する。
このとき、\(y^{\prime}_{p}=-2C\mathrm{e}^{-2x}\)、\(y^{\prime\prime}=4C\mathrm{e}^{-2x}\) を得る。
これを微分方程式 \(y^{\prime\prime\prime}-3y^{\prime}-2y=\mathrm{e}^{-2x}\) の左辺に代入すると
$$\left(4C\mathrm{e}^{-2x}\right)-3\cdot\left(-2C\mathrm{e}^{-2x}\right)-2\cdot\left(C\mathrm{e}^{-2x}\right)=\mathrm{e}^{-2x}$$
$$\left(4C+6C-2C\right)\mathrm{e}^{-2x}=\mathrm{e}^{-2x}$$
$$8C=1$$
$$C=\displaystyle\frac{1}{8}$$
従って \(y_{p}=\displaystyle\frac{1}{8}\mathrm{e}^{-2x}\) は問題の微分方程式の特殊解となる。
No.3 : 「 \(=0\) 」の一般解 \(y_{0}\) と「 \(=\mathrm{e}^{-2x}\) 」の特殊解を足して真の解を導く
求める微分方程式の解 \(y\) は No.1 で得た「 \(=0\) 」の一般解 \(y_{0}\) と No.2 で得た「 \(=\mathrm{e}^{-2x}\) 」 の特殊解 \(y_{p}\) の和である。
\begin{eqnarray}y&=&y_{0}+y_{p}\\\\&=&\left(C_{1}+C_{2}x\right)\mathrm{e}^{-x}+C_{3}\mathrm{e}^{2x}+\displaystyle\frac{1}{8}\mathrm{e}^{-2x}\end{eqnarray}
真の解はなぜ一般解と特殊解の和なのか?という疑問に対しては下記事で解説している(「なぜ一般解と特殊解を足すのか?」の項目参照)
練習問題
練習問題1
\(y^{\prime\prime\prime}-3y^{\prime\prime}+3y^{\prime}-y=0\) を解け。
練習問題2
\(y^{\prime\prime\prime\prime}-2y^{\prime\prime\prime}+2y^{\prime\prime}-2y^{\prime}+1=\sin{x}\) を解け。
ひとこと
多くの微分方程式は今回紹介した「解予想」の方法で解くことができる。少々係数比較の連立方程式がめんどくさいかもしれないが、「微分演算子法」よりは直感的・単純に微分方程式を解き進めることができる。
しかし、荒削りな解法なだけに「微分演算子法」よりは対応できる微分方程式の種類が限られる点に注意!!「べき関数」「指数関数」「三角関数」であれば「解予想法」を使うことができるが、右辺が対数関数であったり複数の関数の組み合わせであると使えなくなってしまう。
.jpg)





