ベルヌーイ型微分方程式
次の形の微分方程式を考えよう。
$$y’+p(x)y=q(x)y^{n}$$
\(y^n\) さえなければ 一階線形微分方程式 の形である。
このような形の微分方程式を ベルヌーイ型微分方程式 という。
解法を確認して、例題を解いていこう。
解法
No.1 : 両辺を \(y^{n}\) で割る
$$y’y^{-n}+p(x)y^{1-n}=q(x)$$
No.2 : \(u=y^{1-n}\) と置く。 ( \(p(x)\) の係数を \(u\) と置く。)
\(u=y^{1-n}\) と置くと \(x\) で微分したとき
\begin{eqnarray}\displaystyle\frac{du}{dx}&=&\left(1-n\right)\cdot y^{\{\left(1-n\right)-1\}}\cdot\displaystyle\frac{dy}{dx}\\&=&\left(1-n\right)\cdot y^{-n}\cdot\displaystyle\frac{dy}{dx}\end{eqnarray}
すなわち
$$u’=\left(1-n\right)\cdot y^{-n}\cdot y’\cdot\cdot\cdot\left(A\right)$$
No.3 : No.2 で得た式を使い \(y\) から \(u\) へ選手交代
\(\left(A\right)\)式から
$$y^{-n}y’=\displaystyle\frac{u’}{1-n}$$
を得るので、これと \(u=y^{1-n}\) を元の式に代入して
$$\displaystyle\frac{1}{1-n}\times u’+p(x)u=q(x)$$
$$u’+\left(1-n\right)p(x)\times u=\left(1-n\right)q(x)$$
ここで、\(P(x)=\left(1-n\right)p(x)\)、\(Q(x)=\left(1-n\right)q(x)\)と置くと、
$$u’+P(x)u=Q(x)$$
となり、これは一階線形微分方程式である。つまりベルヌーイ型微分方程式は、\(u=y^{1-n}\) と置くことで一階線形微分方程式の形に帰着できる。
No.4 : 一階線形微分方程式の解法を用いて解き進める。
1階線形微分方程式の解き方を適用して解を得る。
例題
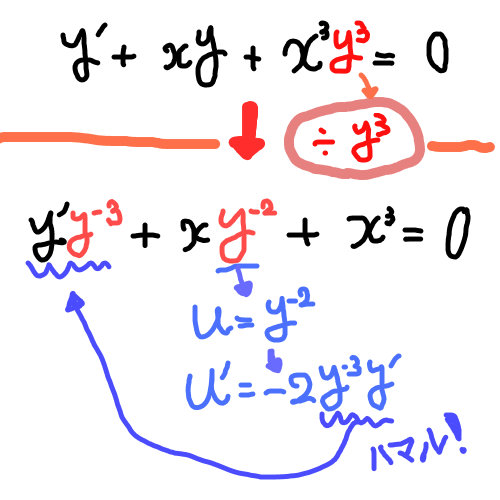
\(y’+xy+x^{3}y^{3} =0\) を解け。
例題の解答
No.1 : 両辺を \(y^{3}\) で割る
左辺の三番目の項を右辺へ移動させて
$$y’+xy=-x^{3}y^{3}$$
両辺を \(y^{3}\) で割ると
$$y’y^{-3}+xy^{-2}=-x^{3}$$
まず問題の微分方程式を、
\(y’+\) ( \(x\) の関数) \(y\) = [ \(x\) の関数 ] \(y^n\)
の形に整理すると何で割るか見通しが立つ。
No.2 : \(u=y^{-2}\) と置く。
\(u=y^{-2}\) と置き \(x\) で微分すると
\begin{eqnarray}\displaystyle\frac{du}{dx}&=&-2\cdot y^{\left(-2-1\right)}\cdot \displaystyle\frac{dy}{dx}\\&=& -2\ y^{-3}\displaystyle\frac{dy}{dx}\end{eqnarray}
すなわち
$$u’=-2\ y^{-3}\ y’\cdot\cdot\cdot\left(B\right)$$
\(u\) の置き方でミスらないように!
No.1 で作った式 \(y’y^{-3}+xy^{-2}=-x^{3}\) において、\(y^{-3}\) を \(u\) とおいてもうまくいかない。。
\(y’\) がついてない方の \(y^{-2}\) を \(u\) と置くことに注意しよう!
No.3 : No.2 で得た式を使い \(y\) から \(u\) へ選手交代
\(\left(C\right)\) 式から
$$y^{-3}y’=-\displaystyle\frac{1}{2}u’$$
を得るので、これと \(u=y^{-2}\) を \(\left(B\right)\) 式に代入して
$$-\displaystyle\frac{1}{2}u’+xu=-x^3$$
\(u’\) の係数は1にするとわかりやすいので、両辺に \(-2\) をかけて
$$u’-2xu=2x^3$$
見事に 一階線形微分方程式 の形に帰着できた。
No.4 : 一階線形微分方程式の解法を用いて解き進める。
ここからは 一階線形微分方程式の解法 に則って解き進める。
まず両辺に \(x\) の関数 \(\mu(x)\) をかける。
$$\mu u’-2\mu xu=2\mu x^3$$
ここで、\(\mu\) が \(-2\mu x=\mu’\) を満たすものと設定すると、
$$\mu u’+\mu’ u=2\mu x^3$$
\(\mu u’+\mu’ u=\left(\mu\cdot u\right)’\) より
$$\left(\mu\cdot u\right)’=2\mu x^3\cdot\cdot\cdot\left(D\right)$$
今、\(\mu\) について、\(-2\mu x=\mu’\) すなわち \(-2\mu x=\displaystyle\frac{d\mu}{dx}\) であるので左辺に \(x\)、右辺に \(\mu\) について変数分離してあげて
$$-2xdx=\displaystyle\frac{1}{\mu}d\mu$$
$$\int\left(-2x\right)dx=\int\displaystyle\frac{1}{\mu}d\mu$$
$$-x^2=\log{\mu}$$
$$\mu=\mathrm{e}^{-x^2}$$
\(\left(D\right)\) 式に今求めた \(\mu=\mathrm{e}^{-x^2}\) を代入して
$$\left(\mathrm{e}^{-x^2}\cdot u\right)=2\mathrm{e}^{-x^2} x^3$$
両辺を \(x\) で積分すると
$$\mathrm{e}^{-x^2}\cdot u=\int\left(2\mathrm{e}^{-x^2}x^{3}\right)dx\cdot\cdot\cdot\left(E\right)$$
右辺の積分だが、\(t=x^2\) と置換して積分することで計算できる。
\(t=x^2\) と置くと、\(\displaystyle\frac{dt}{dx}=2x\) つまり
$$dt=2xdx$$
よって、\(\int\left(2\mathrm{e}^{-x^2}x^{3}\right)dx\) に代入して
\begin{eqnarray}\int\left(2\mathrm{e}^{-x^2}x^{3}\right)dx&=&\int\left(\mathrm{e}^{-x^2}\cdot x^2\right)\cdot 2xdx\\&=&\int\left(\mathrm{e}^{-t}\cdot t\right)dt\\&=&-\left(t+1\right)\ \mathrm{e}^{-t}+C\\&=&-\left(x^2+1\right)\mathrm{e}^{-x^2}+C\end{eqnarray}
ただし、\(C\) は積分定数とする。
\(\left(E\right)\) 式は
$$\mathrm{e}^{-x^2}\cdot u=-\left(x^2+1\right)\mathrm{e}^{-x^2}+C$$
両辺に \(\mathrm{e}^{x^2}\) をかけて
$$u=-x^2+1+C\mathrm{e}^{x^2}$$
No.5 : \(u=y^{-2}\) を代入し直す。
No.4 で得た \(u\) についての解に \(u=y^{-2}\) を代入して
$$y^{-2}=-x^2+1+C\mathrm{e}^{x^2}$$
$$y^2=\displaystyle\frac{1}{-x^2+1+C\mathrm{e}^{x^2}}$$
$$y=\displaystyle\frac{1}{\sqrt{-x^2+1+C\mathrm{e}^{x^2}}}$$
練習問題
練習問題
\(y’+\displaystyle\frac{y}{x}-x^{2}y^{5}=0\) を解け。
ひとこと
ベルヌーイ型微分方程式 は置き換えを用いて一階線形微分方程式に帰着させて攻略していく。
\(u=y^{1-n}\) と置くことで、\(u’=\left(1-n\right)y^{-n}y’\) つまり \(y^{-n}y’=\displaystyle\frac{1}{1-n}u’\) を得る。
これより、\(y’y^{-n}+p(x)y^{1-n}=q(x)\) にすっぽり \(u\) の式を代入することができる。